Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Мерзляк ФГОС Проверь себя 5
Проверь себя 5
\[\boxed{\text{Задание}\text{\ 5.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\boxed{\mathbf{1.}}\]
\[\mathbf{А})\ x^{2} = \ 0 \Longrightarrow квадратное.\]
\[Б)\ x^{2} + x = 0 \Longrightarrow квадратное.\]
\[В)\ x^{3} + x = 0 \Longrightarrow не\ \]
\[квадратное.\]
\[Г)\ x^{2} + x - 2 = 0 \Longrightarrow\]
\[\Longrightarrow квадратное.\]
\[Ответ:В).\]
\[\boxed{\mathbf{2.}}\]
\[9x - x^{2} = 0\]
\[x(9 - x) = 0\]
\[x = 0;\ \ \ x = 9\]
\[Ответ:Г).\]
\[\boxed{\mathbf{3.}}\]
\[\frac{x^{2} - x}{6} - \frac{x - 2}{3} = \frac{3 - x}{2}\ \ \ \ \ \ \ \ | \cdot 6\]
\[x^{2} - x - 2x + 4 - 9 + 3x = 0\]
\[x^{2} - 5 = 0\]
\[x^{2} = 5\]
\[x = \sqrt{5};\ \ \ \ x = - \sqrt{5}\]
\[Ответ:Г).\]
\[\boxed{\mathbf{4.}}\]
\[А)\ x^{2} - 5x - 2 = 0\]
\[\ D = 25 + 8 > 0\]
\[два\ корня.\]
\[Б)\ x^{2} - 5x + 2 = 0,\ \]
\[\ D = 25 - 8 > 0\]
\[два\ корня.\]
\[В)\ x^{2} - 2x + 5 = 0,\]
\[\ D = 4 - 20 < 0\]
\[нет\ корней.\]
\[Г)\ x^{2} + 2x - 5 = 0,\ \]
\[\ D = 4 + 20 > 0\]
\[два\ корня.\]
\[Ответ:В).\]
\[\boxed{\mathbf{5.}}\]
\[6x^{2} + 13x + 5 = 0\]
\[D = 169 - 120 = 49 > 0 - два\ \]
\[корня.\]
\[Ответ:А).\]
\[\boxed{\mathbf{6.}}\]
\[x^{2} + 4x - 21 = 0\]
\[D = 16 + 84 = 100\]
\[x = \frac{- 4 \pm 10}{2}\]
\[x = - 7;\ \ x = 3\]
\[Ответ:Б).\]
\[\boxed{\mathbf{7.}}\]
\[x^{2} - 10x - 12 = 0\]
\[По\ теореме\ Виета:\]
\[x_{1} + x_{2} = 10\]
\[Ответ:А).\]
\[\boxed{\mathbf{8.}}\]
\[3x^{2} - 16x + 6 = 0\ \ \ \ \ \ |\ :3\]
\[x^{2} - \frac{16}{3}x + 2 = 0\]
\[x_{1} \cdot x_{2} = c = 2\]
\[Ответ:Б).\]
\[\boxed{\mathbf{9.}}\]
\[(3x - 1)(x + 2) =\]
\[= (x - 12)(x - 4)\]
\[3x^{2} + 6x - x - 2 =\]
\[= x^{2} - 4x - 12x + 48\]
\[2x^{2} + 21x - 50 = 0\]
\[D = 441 + 400 = 841 = 29²\]
\[x_{1} = \frac{- 21 + 29}{4} = \frac{8}{4} = 2;\ \ \ \ \ \]
\[x_{2} = \frac{- 21 - 29}{4} = - \frac{50}{4} = - 12,5\]
\[Ответ:А).\]
\[\boxed{\mathbf{10.}}\]
\[x_{1} = 3 - \sqrt{2};\ \ \ \ \ \ \ \ \ \ x_{2} = 3 + \sqrt{2}\]
\[x_{1} \cdot x_{2} = c =\]
\[= \left( 3 - \sqrt{2} \right)\left( 3 + \sqrt{2} \right) = 9 - 2 =\]
\[= 7\]
\[x_{1} + x_{2} = - b =\]
\[= 3 - \sqrt{2} + 3 + \sqrt{2} = 6\]
\[x^{2} - 6x + 7 = 0\]
\[Ответ:Г).\]
\[\boxed{\mathbf{11.}}\]
\[x|x| - 9x - 10 = 0\]
\[Ответ:Б).\]
\[\boxed{\mathbf{12.}}\]
\[2x^{2} + 9x + c = 0\]
\(\left\{ \begin{matrix} x_{1} = - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \\ x_{1} \cdot x_{2} = c\ :2\ \ \ \\ x_{1} + x_{2} = - 4,5 \\ \end{matrix} \right.\ \)
\[x_{2} = - 4,5 - x_{1} = - 4,5 + 5 = 0,5\]
\[x_{1} \cdot x_{2} = - 5 \cdot 0,5 = - 2,5\]
\[c = - 2,5 \cdot 2 = - 5\]
\[Ответ:А).\]
\[\boxed{\text{Задание}\text{\ 5.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\boxed{\mathbf{1.}}\]
\[\mathbf{А})\ x^{2} = \ 0 \Longrightarrow квадратное.\]
\[Б)\ x^{2} + x = 0 \Longrightarrow квадратное.\]
\[В)\ x^{3} + x = 0 \Longrightarrow не\ \]
\[квадратное.\]
\[Г)\ x^{2} + x - 2 = 0 \Longrightarrow\]
\[\Longrightarrow квадратное.\]
\[Ответ:В).\]
\[\boxed{\mathbf{2.}}\]
\[9x - x^{2} = 0\]
\[x(9 - x) = 0\]
\[x = 0;\ \ \ x = 9\]
\[Ответ:Г).\]
\[\boxed{\mathbf{3.}}\]
\[\frac{x^{2} - x}{6} - \frac{x - 2}{3} = \frac{3 - x}{2}\ \ \ \ \ \ \ \ | \cdot 6\]
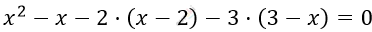
\[x^{2} - x - 2x + 4 - 9 + 3x = 0\]
\[x^{2} - 5 = 0\]
\[x^{2} = 5\]
\[x = \sqrt{5};\ \ \ \ x = - \sqrt{5}\]
\[Ответ:Г).\]
\[\boxed{\mathbf{4.}}\]
\[А)\ x^{2} - 5x - 2 = 0\]
\[\ D = 25 + 8 > 0\]
\[два\ корня.\]
\[Б)\ x^{2} - 5x + 2 = 0,\ \]
\[\ D = 25 - 8 > 0\]
\[два\ корня.\]
\[В)\ x^{2} - 2x + 5 = 0,\]
\[\ D = 4 - 20 < 0\]
\[нет\ корней.\]
\[Г)\ x^{2} + 2x - 5 = 0,\ \]
\[\ D = 4 + 20 > 0\]
\[два\ корня.\]
\[Ответ:В).\]
\[\boxed{\mathbf{5.}}\]
\[6x^{2} + 13x + 5 = 0\]
\[D = 169 - 120 = 49 > 0 - два\ \]
\[корня.\]
\[Ответ:А).\]
\[\boxed{\mathbf{6.}}\]
\[x^{2} + 4x - 21 = 0\]
\[D = 16 + 84 = 100\]
\[x = \frac{- 4 \pm 10}{2}\]
\[x = - 7;\ \ x = 3\]
\[Ответ:Б).\]
\[\boxed{\mathbf{7.}}\]
\[x^{2} - 10x - 12 = 0\]
\[По\ теореме\ Виета:\]
\[x_{1} + x_{2} = 10\]
\[Ответ:А).\]
\[\boxed{\mathbf{8.}}\]
\[3x^{2} - 16x + 6 = 0\ \ \ \ \ \ |\ :3\]
\[x^{2} - \frac{16}{3}x + 2 = 0\]
\[x_{1} \cdot x_{2} = c = 2\]
\[Ответ:Б).\]
\[\boxed{\mathbf{9.}}\]
\[(3x - 1)(x + 2) =\]
\[= (x - 12)(x - 4)\]
\[3x^{2} + 6x - x - 2 =\]
\[= x^{2} - 4x - 12x + 48\]
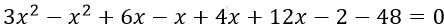
\[2x^{2} + 21x - 50 = 0\]
\[D = 441 + 400 = 841 = 29²\]
\[x_{1} = \frac{- 21 + 29}{4} = \frac{8}{4} = 2;\ \ \ \ \ \]
\[x_{2} = \frac{- 21 - 29}{4} = - \frac{50}{4} = - 12,5\]
\[Ответ:А).\]
\[\boxed{\mathbf{10.}}\]
\[x_{1} = 3 - \sqrt{2};\ \ \ \ \ \ \ \ \ \ x_{2} = 3 + \sqrt{2}\]
\[x_{1} \cdot x_{2} = c =\]
\[= \left( 3 - \sqrt{2} \right)\left( 3 + \sqrt{2} \right) = 9 - 2 =\]
\[= 7\]
\[x_{1} + x_{2} = - b =\]
\[= 3 - \sqrt{2} + 3 + \sqrt{2} = 6\]
\[x^{2} - 6x + 7 = 0\]
\[Ответ:Г).\]
\[\boxed{\mathbf{11.}}\]
\[x^{2} + 3x + \frac{2}{x + 4} = 4 + \frac{2}{x + 4};\ x \neq - 4\]
\[x^{2} + 3x - 4 = 0\]
\[x_{1} + x_{2} = - 3;\ \ x_{1} \cdot x_{2} = - 4\]
\[x_{1} = - 4\ (не\ подходит);\]
\[x_{2} = 1.\]
\[Ответ:Б)\ 1.\]
\[\boxed{\mathbf{12.}}\]
\[2x^{2} + 9x + c = 0\]
\(\left\{ \begin{matrix} x_{1} = - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \\ x_{1} \cdot x_{2} = c\ :2\ \ \ \\ x_{1} + x_{2} = - 4,5 \\ \end{matrix} \right.\ \)
\[x_{2} = - 4,5 - x_{1} = - 4,5 + 5 = 0,5\]
\[x_{1} \cdot x_{2} = - 5 \cdot 0,5 = - 2,5\]
\[c = - 2,5 \cdot 2 = - 5\]
\[Ответ:А).\]
