Решебник по алгебре 8 класс Макарычев ФГОС Задание 984

 

\[\boxed{\text{984\ (984).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Координаты точки – это пара чисел, в которой на первом месте стоит абсцисса (x), а на втором – ордината точки (у): A (x; y).

Вид функции обратной пропорциональности:\(\ \)

\[\mathbf{y =}\frac{\mathbf{k}}{\mathbf{x}}\mathbf{.}\]

Чтобы найти коэффициент обратной пропорциональности (k), нужно данные координаты точки подставить в функцию и решить её.

Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

Решение.

\[\textbf{а)}\ А\ (1,5;8);\ \ y = \frac{k}{x}\]

\[x = 1,5;\ \ y = 8\]

\[8 = \frac{k}{1,5}\ \ \ \ \ | \cdot 1,5\]

\[k = 12.\]

\[\textbf{б)}\ В\ (0,04;\ - 25);\ \ y = \frac{k}{x}\]

\[x = 0,04;\ \ \ y = - 25\]

\[- 25 = \frac{k}{0,04}\ \ \ \ \ | \cdot 0,04\]

\[k = - 1.\]

\[\boxed{\text{984.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[\textbf{а)}\ \left\{ \begin{matrix} 5 \cdot (x - 2) - x > 2 \\ 1 - 3 \cdot (x - 1) < - 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 5x - 10 - x > 2 \\ 1 - 3x + 3 < - 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 4x > 12 \\ - 3x < - 6 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > 3 \\ x > 2 \\ \end{matrix} \right.\ \Longrightarrow \ \ (3;\ + \infty)\]

\[\textbf{б)}\ \left\{ \begin{matrix} 2y - (y - 4) < 6\ \ \ \ \ \ \ \\ y > 3 \cdot (2y - 1) + 18 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 2y - y + 4 < 6 \\ y > 6y - 3 + 18 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} y < 2\ \ \ \ \ \ \ \ \\ - 5y > 15 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} y < 2\ \ \ \\ y < - 3 \\ \end{matrix} \right.\ \Longrightarrow \text{\ \ }( - \infty;\ - 3)\]

\[\textbf{в)}\ \left\{ \begin{matrix} 7x + 3 \geq 5 \cdot (x - 4) + 1 \\ 4x + 1 \leq 43 - 3 \cdot (7 + x) \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 7x + 3 \geq 5x - 20 + 1 \\ 4x + 1 \leq 43 - 21 - 3x \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 2x \geq - 22 \\ 7x \leq 21\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

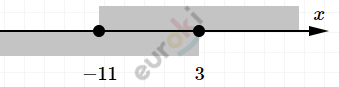
\[\left\{ \begin{matrix} x \geq - 11 \\ x \leq 3\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \ \ \lbrack - 11;3\rbrack\]

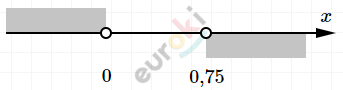
\[\textbf{г)}\ \left\{ \begin{matrix} 3 \cdot (2 - 3p) - 2 \cdot (3 - 2p) > p \\ 6 < p^{2} - p(p - 8)\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\ \left\{ \begin{matrix} 6 - 9p - 6 + 4p > p \\ 6 < p^{2} - p^{2} + 8p\ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} - 6p > 0 \\ 6 < 8p\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\ \left\{ \begin{matrix} p < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ p > \frac{6}{8} > 0,75 \\ \end{matrix} \right.\ \Longrightarrow нет\ решений.\]