Решебник по алгебре 8 класс Макарычев ФГОС Задание 980

 

\[\boxed{\text{980\ (980).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Степень с отрицательным показателем – это дробь, числителем которой является единица, а знаменателем – данное число с положительным показателем:

\[\mathbf{a}^{\mathbf{- n}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{a}^{\mathbf{n}}}\mathbf{.}\]

При решении используем следующее:

1. Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести их к наименьшему общему знаменателю, затем сложить (вычесть) числители дробей, а знаменатель оставить без изменений.

2. Чтобы привести дроби к наименьшему общему знаменателю используем правило:

1. Найти наименьший общий знаменатель, который делится на каждый из знаменателей без остатка.

2. Найти дополнительный множитель, для каждого числителя, разделив общий знаменатель на знаменатели данных дробей.

3. Умножить числитель каждой дроби на дополнительный множитель.

3. Формулу умножения многочлена на многочлен – каждое число из первой скобки умножить на каждое число из второй:

\[\left( \mathbf{a + b} \right)\left( \mathbf{c + d} \right)\mathbf{= ac + ad + bc + bd.}\]

4. Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй дроби, также умножить знаменатели. Первое произведение записать числителем, а второе – знаменателем:

\[\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\bullet}\frac{\mathbf{c}}{\mathbf{d}}\mathbf{=}\frac{\mathbf{\text{ac}}}{\mathbf{\text{bd}}}\]

Решение.

\[\textbf{а)}\ a^{- 2} + b^{- 2} = \frac{1}{a^{2}} + \frac{1}{b^{2}} =\]

\[= \frac{b^{2} + a^{2}}{a^{2}b^{2}}\]

\[\textbf{б)}\ xy^{- 1} + xy^{- 2} = \frac{x}{y} + \frac{x}{y^{2}} =\]

\[= \frac{xy + x}{y^{2}}\]

\[\textbf{в)}\ \left( a + b^{- 1} \right)\left( a^{- 1} - b \right) =\]

\[= \left( a + \frac{1}{b} \right)\left( \frac{1}{a} - b \right) =\]

\[= \frac{a}{a} - ab + \frac{1}{\text{ab}} - \frac{b}{b} =\]

\[= 1 - ab + \frac{1}{\text{ab}} - 1 = \frac{- a^{2}b^{2} + 1}{\text{ab}}\]

\[\textbf{г)}\ \left( x - 2y^{- 1} \right)\left( x^{- 1} + 2y \right) =\]

\[= \left( x - \frac{2}{y} \right)\left( \frac{1}{x} + 2y \right) =\]

\[= \frac{xy - 2}{y} \cdot \frac{1 + 2xy}{x} =\]

\[= \frac{(xy - 2)(1 + 2xy)}{\text{xy}}\]

\[\boxed{\text{980.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[\textbf{а)}\ \left\{ \begin{matrix} 2x - 1 < 1,4 - x \\ 3x - 2 > x - 4\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 2x + x < 1,4 + 1 \\ 3x - x > - 4 + 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\ \left\{ \begin{matrix} 3x < 2,4 \\ 2x > - 2 \\ \end{matrix} \right.\ \text{\ \ \ }\]

\[\ \left\{ \begin{matrix} x < 0,8 \\ x > - 1 \\ \end{matrix} \right.\ \Longrightarrow ( - 1;0,8)\]

\[\textbf{б)}\ \left\{ \begin{matrix} 5x + 6 \leq x\ \ \ \ \ \ \ \ \ \ \ \ \\ 3x + 12 \leq x + 17 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 5x - x \leq - 6\ \ \ \ \ \ \ \ \ \\ 3x - x \leq 17 - 12 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 4x \leq - 6 \\ 2x \leq 5\ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq - \frac{6}{4} \\ x \leq 2,5 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\text{\ \ }\left\{ \begin{matrix} x \leq - 1,5 \\ x \leq 2,5\ \ \ \\ \end{matrix} \right.\ \Longrightarrow \ \ ( - \infty; - 1,5\rbrack.\]

\[\textbf{в)}\ \left\{ \begin{matrix} 17x - 2 > 12x - 1 \\ 3 - 9x < 1 - x\ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 17x - 12x > - 1 + 2 \\ - 9x + x < 1 - 3\ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 5x > 1\ \ \ \ \\ - 8x < - 2 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{1}{5} \\ x > \frac{2}{8} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

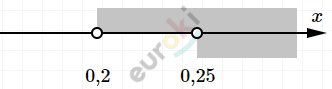
\[\left\{ \begin{matrix} x > 0,2\ \ \\ x > 0,25 \\ \end{matrix} \right.\ \Longrightarrow \ (0,25;\ + \infty)\]

\[\textbf{г)}\ \left\{ \begin{matrix} 25 - 6x \leq 4 + x \\ 3x + 7,7 > 1 + 4x \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} - 6x - x \leq 4 - 25 \\ 3x - 4x > 1 - 7,7 \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\ \left\{ \begin{matrix} - 7x \leq - 21 \\ - x > - 6,7 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq 3\ \ \ \\ x < 6,7 \\ \end{matrix} \right.\ \Longrightarrow \text{\ \ }\lbrack 3;6,7)\]