Решебник по алгебре 8 класс Макарычев ФГОС Задание 975

 

\[\boxed{\text{975\ (975).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Чтобы найти значение выражения при данном значении переменной (буквы y, x и тд.), надо подставить в буквенное выражение (вместо y, x и тд.) данное значение и выполнить вычисление.

аⁿ (а в n-ой степени) – число «n» называют показателем степени, а число «а» – основанием степени. Степень говорит нам о том, сколько раз следует умножить число «a» само на себя. Например, 3⁴=3*3*3*3=81.

Степень с отрицательным показателем – это дробь, числителем которой является единица, а знаменателем – данное число с положительным показателем:

\[\mathbf{a}^{\mathbf{- n}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{a}^{\mathbf{n}}}\mathbf{.}\]

При решении используем следующее:

1. При возведении отрицательного числа в степень с чётным показателем (число, которое делится на 2 без остатка) получается положительное число:

\[\mathbf{(}\mathbf{- 3)}^{\mathbf{4}}\mathbf{= 81.}\]

2. При возведении отрицательного числа в степень с нечётным показателем (число, которое не делится на 2 без остатка) получается отрицательное число:

\[\mathbf{(}\mathbf{- 3)}^{\mathbf{3}}\mathbf{= - 27.}\]

3. Чтобы возвести дробь в отрицательную степень, нужно поменять местами числитель со знаменателем, а после возвести в степень уже без знака « – »:

\[\left( \frac{\mathbf{a}}{\mathbf{b}} \right)^{\mathbf{- n}}\mathbf{=}\left( \frac{\mathbf{b}}{\mathbf{a}} \right)^{\mathbf{n}}\mathbf{.}\]

4. Чтобы возвести дробь в степень, необходимо возвести в эту степень числитель и знаменатель:

\[\left( \frac{\mathbf{a}}{\mathbf{b}} \right)^{\mathbf{n}}\mathbf{=}\frac{\mathbf{a}^{\mathbf{n}}}{\mathbf{b}^{\mathbf{n}}}\mathbf{.}\]

5. Чтобы десятичную дробь перевести в обыкновенную, нужно число после запятой поставить в числитель, а в знаменателе 10, 100, 1000 и т.д. (количество нулей зависит от того, сколько цифр после запятой).

Например, \(\mathbf{0,125 =}\frac{\mathbf{125}}{\mathbf{1000}}\mathbf{.}\ \)

Решение.

\[x^{n} = ?,\ \ x^{- n} = ?\]

\[\textbf{а)}\ x = \frac{2}{3},\ \ n = - 2\]

\[x^{n} = \left( \frac{2}{3} \right)^{- 2} = \left( \frac{3}{2} \right)^{2} = \frac{9}{4}\]

\[x^{- n} = \left( \frac{2}{3} \right)^{- ( - 2)} = \left( \frac{2}{3} \right)^{2} = \frac{4}{9}\]

\[\textbf{б)}\ x = - 1,5,\ \ n = 3\]

\[x^{n} = ( - 1,5)^{3} = \left( - \frac{3}{2} \right)^{3} = - \frac{27}{8}\]

\[x^{- n} = ( - 1,5)^{- 3} = \left( - \frac{3}{2} \right)^{- 3} =\]

\[= \left( - \frac{2}{3} \right)^{3} = - \frac{8}{27}\]

\[\boxed{\text{975.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[\textbf{а)}\ \left\{ \begin{matrix} x > 17 \\ x > 12 \\ \end{matrix} \right.\ \Longrightarrow \ \ (17;\ + \infty)\]

\[\textbf{б)}\ \left\{ \begin{matrix} x < 1 \\ x < 5 \\ \end{matrix} \right.\ \Longrightarrow \ \ ( - \infty;1)\]

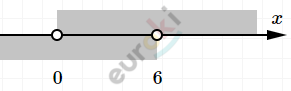
\[\textbf{в)}\ \left\{ \begin{matrix} x > 0 \\ x < 6 \\ \end{matrix} \right.\ \Longrightarrow \ \ (0;6)\]

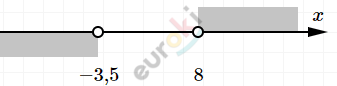
\[\textbf{г)}\ \left\{ \begin{matrix} x < - 3,5 \\ x > 8 \\ \end{matrix} \right.\ \Longrightarrow нет\ решений\]

\[\textbf{д)}\ \left\{ \begin{matrix} x \geq - 1 \\ x \leq 3 \\ \end{matrix} \right.\ \Longrightarrow \ \ \lbrack - 1;3\rbrack\]

\[\textbf{е)}\ \left\{ \begin{matrix} x > 8 \\ x \leq 20 \\ \end{matrix} \right.\ \Longrightarrow \ \ (8;20\rbrack\]