Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 876
Задание 876
\[\boxed{\text{876\ (876).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
| Неравенство, задающее числовой промежуток. | Обозначение и название числового промежутка. | Изображение числового промежутка на координатной прямой. |
|---|---|---|
| \[\mathbf{a \leq x \leq b}\] |
\[\left\lbrack \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[числовой\ отрезок\ \] |
 |
| \[\mathbf{a < x < b}\] |
\[\left( \mathbf{a;\ b} \right)\mathbf{- \ }\] \[\mathbf{интервал}\] |
 |
| \[\mathbf{a \leq x < b}\] |
\[\left\lbrack \mathbf{a;\ b} \right)\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{a < x \leq b}\] |
\[\left( \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{x \geq a}\] |
\[\left\lbrack \mathbf{a; + \infty} \right)\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
| \[\mathbf{x > a}\] |
\[\mathbf{(a; + \infty) -}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
| \[\mathbf{x \leq b}\] |
\[\left( \mathbf{- \infty;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
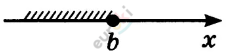| \[\mathbf{x < b}\] |
\[\left( \mathbf{- \infty;\ b} \right)\mathbf{-}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
Решение.
\[\textbf{а)}\ \left\{ \begin{matrix} x > 17 \\ x > 12 \\ \end{matrix} \right.\ \Longrightarrow \ \ (17;\ + \infty)\]
\[\textbf{б)}\ \left\{ \begin{matrix} x < 1 \\ x < 5 \\ \end{matrix} \right.\ \Longrightarrow \ \ ( - \infty;1)\]
\[\textbf{в)}\ \left\{ \begin{matrix} x > 0 \\ x < 6 \\ \end{matrix} \right.\ \Longrightarrow \ \ (0;6)\]
\[\textbf{г)}\ \left\{ \begin{matrix} x < - 3,5 \\ x > 8 \\ \end{matrix} \right.\ \Longrightarrow нет\ решений\]
\[\textbf{д)}\ \left\{ \begin{matrix} x \geq - 1 \\ x \leq 3 \\ \end{matrix} \right.\ \Longrightarrow \ \ \lbrack - 1;3\rbrack\]
\[\textbf{е)}\ \left\{ \begin{matrix} x > 8 \\ x \leq 20 \\ \end{matrix} \right.\ \Longrightarrow \ \ (8;20\rbrack\]
\[\boxed{\text{876.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[\textbf{а)}\ \sqrt{2} + 5\ и\ 2 + \sqrt{5}\]
\[\sqrt{1} + 5 < \sqrt{2} + 5 < \sqrt{4} + 5\]
\[6 < \sqrt{2} + 5 < 7.\]
\[2 + \sqrt{4} < 2 + \sqrt{5} < 2 + \sqrt{9}\]
\[4 < 2 + \sqrt{5} < 5.\]
\[\sqrt{2} + 5 > 2 + \sqrt{5}.\]
\[\textbf{б)}\ \sqrt{3} - 4\ \ и\ 1 - \sqrt{5}\]
\[\sqrt{1} - 4 < \sqrt{3} - 4 < \sqrt{4} - 4\]
\[- 3 < \sqrt{3} - 4 < - 2.\]
\[1 - \sqrt{4} < 1 - \sqrt{5} < 1 - \sqrt{9}\]
\[- 1 > 1 - \sqrt{5} > - 2\]
\[- 2 < 1 - \sqrt{5} < - 1.\]
\[\sqrt{3} - 4 < 1 - \sqrt{5}\]
\[\textbf{в)}\frac{2\sqrt{3} + 23}{3}\ и\ 9\]
\[\sqrt{1} < \sqrt{3} < \sqrt{4}\]
\[1 < \sqrt{3} < 2.\]
\[2 \cdot 1 + 23 < 2\sqrt{3} +\]
\[+ 23 < 2 \cdot 2 + 23\]
\[25 < 2\sqrt{3} + 23 < 27\]
\[\frac{25}{3} < \frac{2\sqrt{3} + 23}{3} < 9.\]
\[\frac{2\sqrt{3} + 23}{3} < 9.\]
\[\textbf{г)}\frac{1 - \sqrt{15}}{12}\ \ и\ \ \left( - \frac{7}{8} \right)\]
\[- \sqrt{16} < - \sqrt{15} < - \sqrt{9}\]
\[- 4 < - \sqrt{15} < - 3.\]
\[\frac{1 - 4}{12} < \frac{1 - \sqrt{15}}{12} < \frac{1 - 3}{12}\]
\[- \frac{3}{12} > \frac{1 - \sqrt{15}}{12} > - \frac{2}{12}\]
\[- \frac{1}{4} > \frac{1 - \sqrt{15}}{12} > - \frac{1}{2}\]
\[- \frac{1}{2} = - \frac{4}{8}\]
\[- \frac{4}{8} > - \frac{7}{8}\]
\[\frac{1 - \sqrt{15}}{12} > - \frac{7}{8}.\]
