Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 846
Задание 846
\[\boxed{\text{846\ (846).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
| Неравенство, задающее числовой промежуток. | Обозначение и название числового промежутка. | Изображение числового промежутка на координатной прямой. |
|---|---|---|
| \[\mathbf{a \leq x \leq b}\] |
\[\left\lbrack \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[числовой\ отрезок\ \] |
 |
| \[\mathbf{a < x < b}\] |
\[\left( \mathbf{a;\ b} \right)\mathbf{- \ }\] \[\mathbf{интервал}\] |
 |
| \[\mathbf{a \leq x < b}\] |
\[\left\lbrack \mathbf{a;\ b} \right)\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{a < x \leq b}\] |
\[\left( \mathbf{a;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{полуинтервал}\] |
 |
| \[\mathbf{x \geq a}\] |
\[\left\lbrack \mathbf{a; + \infty} \right)\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
| \[\mathbf{x > a}\] |
\[\mathbf{(a; + \infty) -}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
| \[\mathbf{x \leq b}\] |
\[\left( \mathbf{- \infty;\ b} \right\rbrack\mathbf{-}\] \[\mathbf{числовой\ луч}\] |
 |
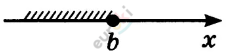| \[\mathbf{x < b}\] |
\[\left( \mathbf{- \infty;\ b} \right)\mathbf{-}\] \[\mathbf{открытый\ числовой\ }\] \[\mathbf{луч}\] |
 |
При решении используем следующее:
1. Если в неравенстве перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится неравенство, равносильное данному.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
4. Распределительное свойство умножения – число, стоящее перед скобкой, нужно умножить на каждое число в скобке:
\[\mathbf{a}\left( \mathbf{b - c} \right)\mathbf{= ab - ac.}\]
Решение.
\[\textbf{а)}\ a(a - 4) - a^{2} > 12 - 6a\]
\[a^{2} - 4a - a^{2} > 12 - 6a\]
\[- 4a + 6a > 12\]
\[2a > 12\]
\[a > 6 \Longrightarrow \ a \in (6;\ + \infty)\]
\[\textbf{б)}\ (2x - 1) \cdot 2x - 5x < 4x^{2} - x\]
\[4x^{2} - 2x - 5x < 4x^{2} - x\]
\[- 2x - 5x + x < 0\]
\[- 6x < 0\]
\[x > 0 \Longrightarrow \ \ x \in (0;\ + \infty)\]
\[\textbf{в)}\ 5y² - 5y(y + 4) \geq 100\]
\[5y^{2} - 5y^{2} - 20y \geq 100\]
\[- 20y \geq 100\]
\[y \leq - 5 \Longrightarrow \ \ y \in ( - \infty;\ - 5\rbrack\]
\[\textbf{г)}\ 6a(a - 1) - 2a(3a - 2) < 6\]
\[6a^{2} - 6a - 6a^{2} + 4a < 6\]
\[- 2a < 6\]
\[a > - 3 \Longrightarrow \ \ a \in ( - 3;\ + \infty)\]
\[\boxed{\text{846.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[\frac{a}{b}\ \ \ \ при\ \ \ \ a < b:\]
\[то\ есть,\ дробь\ уменьшится.\]
\[\frac{a}{b}\ \ \ при\ \ \ a > b:\]
\[\frac{a}{b} - \frac{a + 1}{b + 1} = \frac{a - b}{b(b + 1)} > 0\]
\[то\ есть,\ дробь\ увеличится.\]
