Решебник по алгебре 8 класс Макарычев ФГОС Задание 597

 

\[\boxed{\text{597\ (597).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Катеты\ относятся\ как\ 8\ :15;\ \ \]

\[x - коэффициент.\]

\[Пусть\ 8x\ м - первый\ катет,\ \]

\[тогда\ 15x\ м - второй\ катет.\]

\[Длина\ гипотенузы\ 6,8\ м.\]

\[Составим\ уравнение,\ \]

\[используя\ теорему\ Пифагора:\]

\[(8x)^{2} + (15x)^{2} = {6,8}^{2}\]

\[64x^{2} + 225x^{2} = 46,24\]

\[289x^{2} = 46,24\]

\[x^{2} = \frac{46,24}{289} = \frac{4624}{28900}\]

\[x = \frac{68}{170} = 0,4\]

\[8x = 8 \cdot 0,4 = 3,2\ (м) - первый\ \]

\[катет.\]

\[15x = 15 \cdot 0,4 = 6\ (м) - второй\ \]

\[катет.\]

\[S = \frac{3,2 \cdot 6}{2} = 9,6\ м^{2}.\]

\[Ответ:9,6\ м^{2}\ \]

\[\boxed{\text{597.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

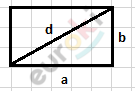
\[d = 34\ см,\ \ b = a + 14\ см\]

\[По\ теореме\ Пифагора:\]

\[a^{2} + (a + 14)^{2} = 34^{2}\]

\[a^{2} + a^{2} + 28a + 196 = 1156\]

\[2a^{2} + 28a - 960 = 0\]

\[a^{2} + 14a - 480 = 0\]

\[D = 196 + 1920 = 2116\]

\[a_{1,2} = \frac{- 14 \pm \sqrt{2116}}{2} = \frac{- 4 \pm 46}{2}\]

\[a_{1} = 16,\ \ a_{2} = - 30 \notin N\]

\[a = 16\ (см) - ширина\ \]

\[прямоугольника.\ \ \]

\[b = 16 + 14 = 30\ (см) - длина\ \]

\[прямоугольника.\]

\[Ответ:16\ см\ и\ 30\ см.\ \ \]