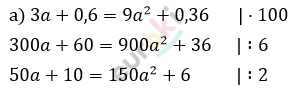Алгебра
Английский
Биология
География
Геометрия
Русский
История
Обществознание
Физика
Химия
Информатика
Литература
МатематикаГДЗ по алгебре 8 класс Макарычев Задание 551
Задание 551
\[\boxed{\text{551\ (551).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
|
\[\textbf{а)}\ 0,7x^{2} = 1,3x + 2\] \[0,7x^{2} - 1,3x - 2 = 0\ \ \ \ \ | \cdot 10\] \[7x^{2} - 13x - 20 = 0\] \[D = 169 + 560 = 729\] \[x_{1,2} = \frac{13 \pm \sqrt{729}}{2 \cdot 7} = \frac{13 \pm 27}{14}\] \[x_{1} = \frac{40}{14} = \frac{20}{7} = 2\frac{6}{7};\] \[x_{2} = - \frac{14}{14} = - 1.\] |
\[\textbf{б)}\ 7 = 0,4y + 0,2y^{2}\ \ \ \ \ \ | \cdot 10\] \[2y^{2} + 4y - 70 = 0\ \ \ \ \ \ |\ :2\] \[y^{2} + 2y - 35 = 0\] \[D = 4 + 140 = 144\] \[y_{1,2} = \frac{- 2 \pm \sqrt{144}}{2 \cdot 1} = \frac{- 2 \pm 12}{2}\] \[y_{1} = - \frac{14}{2} = - 7;\] \[y_{2} = \frac{10}{2} = 5.\] |
|---|---|
|
\[\textbf{в)}\ x^{2} - 1,6x - 0,36 = 0\ \ \ \ \ | \cdot 100\] \[100x^{2} - 160x - 36 = 0\ \ \ \ \ \ |\ :4\] \[25x^{2} - 40x - 9 = 0\] \[D = 1600 + 900 = 2500\] \[x_{1,2} = \frac{40 \pm \sqrt{2500}}{2 \cdot 25} = \frac{40 \pm 50}{50}\] \[x_{1} = \frac{- 10}{50} = - \frac{1}{5} = - 0,2;\] \[x_{2} = \frac{90}{50} = \frac{9}{5} = 1,8.\] |
\[\textbf{г)}\ z^{2} - 2z + 2,91 = 0\ \ \ \ \ \ | \cdot 100\] \[100z^{2} - 200z + 291 = 0\] \[D = 40\ 000 - 116\ 400 < 0\] \[корней\ нет.\] |
|
\[\textbf{д)}\ 0,2y^{2} - 10y + 125 = 0\ \ \ \ \ \ | \cdot 10\] \[2y^{2} - 100y + 1250 = 0\ \ \ \ \ \ \ \ \ \ |\ :2\] \[y^{2} - 50y + 625 = 0\] \[D = 2500 - 2500 = 0\] \[y = \frac{50}{2} = 25.\] |
\[\textbf{е)}\ \frac{1}{3}x^{2} + 2x - 9 = 0\ \ \ \ \ \ | \cdot 3\] \[x^{2} + 6x - 27 = 0\] \[D = 9 + 27 = 36\] \[x_{1,2} = - 3 \pm \sqrt{36}\] \[x_{1} = - 3 + 6 = 3\] \[x_{2} = - 3 - 6 = - 9.\ \] |
