Решебник по алгебре 8 класс Макарычев ФГОС Задание 498

 

\[\boxed{\text{498\ (498).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\sqrt{7 + 4\sqrt{3}} + \sqrt{7 - 4\sqrt{3}} =\]

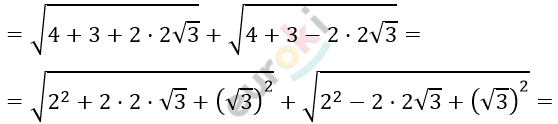
\[= \sqrt{\left( 2 + \sqrt{3} \right)^{2}} + \sqrt{\left( 2 - \sqrt{3} \right)^{2}} =\]

\[= \left| 2 + \sqrt{3} \right| + \left| 2 - \sqrt{3} \right| =\]

\[= 2 + \sqrt{3} + 2 - \sqrt{3} =\]

\[= 4 - натуральное\ число.\]

\[2 + \sqrt{3} > 0;\ \ \ 2 - \sqrt{3} > 0.\]

\[Что\ и\ требовалось\ доказать.\]

\[\sqrt{7 + 4\sqrt{3}} \cdot \sqrt{7 - 4\sqrt{3}} =\]

\[= \sqrt{\left( 7 + 4\sqrt{3} \right)\left( 7 - 4\sqrt{3} \right)} =\]

\[= \sqrt{49 - 16 \cdot 3} = \sqrt{49 - 48} =\]

\[= \sqrt{1} = 1 - натуральное\ число.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\text{498.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

При всех допустимых значениях a верно равенство:

\[\left( \sqrt{a} \right)^{2} = a.\]

Разложим подкоренные выражения на множителе и вынесем общий множитель за скобки.

Корень из произведения неотрицательных множителей (больших или равных 0), равен произведению корней из этих множителей.

\[\sqrt{\text{ab}} = \sqrt{a} \cdot \sqrt{b}.\]

Решение.

\[\textbf{а)}\ \frac{2\sqrt{10} - 5}{4 - \sqrt{10}} = \frac{2\sqrt{5}\sqrt{2} - \sqrt{5}\sqrt{5}}{\sqrt{2}\sqrt{2^{3}} - \sqrt{2}\sqrt{5}} =\]

\[= \frac{\sqrt{5} \cdot \left( 2\sqrt{2} - \sqrt{5} \right)}{\sqrt{2} \cdot \left( 2\sqrt{2} - \sqrt{5} \right)} = \frac{\sqrt{5}}{\sqrt{2}}\ \]

\[\textbf{б)}\ \frac{\left( \sqrt{10} - 1 \right)^{2} - 3}{\sqrt{10} + \sqrt{3} - 1} =\]

\[= \frac{\left( \sqrt{10} - 1 - \sqrt{3} \right)\left( \sqrt{10} - 1 + \sqrt{3} \right)}{\sqrt{10} + \sqrt{3} - 1} =\]

\[= \sqrt{10} - 1 - \sqrt{3}\]