Решебник по алгебре 8 класс Макарычев ФГОС Задание 458

 

\[\boxed{\text{458\ (458).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[Пусть\ \text{n\ }и\ m - целые\ числа,\ \]

\[тогда:\]

\[x = 2n + 1;\ \ y = 2m + 1.\]

\[\textbf{а)}\ x + y = 2n + 1 + 2m + 1 =\]

\[= 2n + 2m + 1 =\]

\[= 2(n + m + 1) - четное.\]

\[\textbf{б)}\ x - y = 2n + 1 - 2m - 1 =\]

\[= 2n - 2m = 2(n - m) -\]

\[четное.\]

\[\textbf{в)}\ xy = (2n + 1)(2m + 1) =\]

\[= 4nm + 2n + 2m + 1 =\]

\[= 2(2nm + n + m) + 1 -\]

\[нечетное.\]

\[\boxed{\text{458.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен a:

\[\sqrt{a} = b\ при\ b \geq 0;b^{2} = a.\]

Решение.

\[\left( \sqrt{x} \right)^{2} = \left( \frac{3}{5} \right)^{2}\]

\[\left( \sqrt{3x} \right)^{2} = \frac{1}{1} = (1)^{2}\]

\[3x = 1\]

\[4\sqrt{x} = \frac{1}{2}\]

\[\left( \sqrt{x} \right)^{2} = \left( \frac{1}{8} \right)^{2}\]

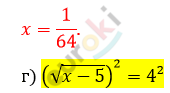
\[x - 5 = 16\]

\[\left( \sqrt{2x} \right)^{2} = 9^{2}\]

\[2x = 81\]

\[3\sqrt{x} = 9\]

\[\left( \sqrt{x} \right)^{2} = 3^{2}\]