Решебник по алгебре 8 класс Макарычев ФГОС Задание 264

 

\[\boxed{\text{264\ (264).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ множество\ четных\ чисел,\ \]

\[не\ кратных\ 3.\]

\[\textbf{б)}\ множество\ делителей\ \]

\[числа\ 18,\ кратных\ 9.\]

\[\textbf{в)}\ множество\ остроугольных\ и\ \]

\[тупоугольных\ треугольников.\]

\[\textbf{г)}\ множество\ \]

\[прямоугольников,\ кроме\ \]

\[квадратов.\]

\[\boxed{\text{264.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Модулем числа a (|a|) называется само число (если a>=0) или противоположное ему число (если a<0):

\[|a| = a;\ \ при\ a \geq 0;\]

\[|a| = - a;\ \ при\ a < 0.\]

В уравнении обратной пропорциональности y=k/x:

\[|x| \neq 0\]

(так как на 0 делить нельзя).

Решение.

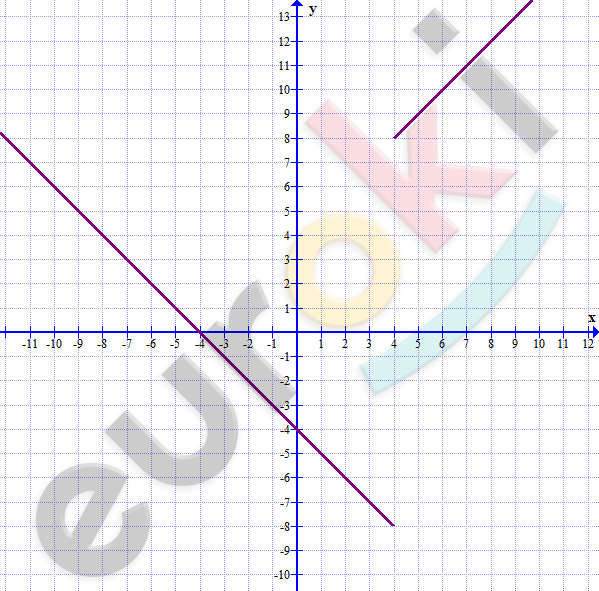
\[\textbf{а)}\ y = \frac{x^{2} - 16}{|x - 4|};\ \ \ \ \ x \neq 4\]

\[При\ x > 4:\]

\[y = \frac{x^{2} - 16}{x - 4} = \frac{(x - 4)(x + 4)}{x - 4} =\]

\[= x + 4.\]

\[При\ x < 4:\]

\[y = \frac{(x - 4)(x + 4)}{- x - 4} =\]

\[= \frac{(x - 4)(x + 4)}{- (x + 4)} = - (x - 4) =\]

\[= - x + 4.\]

\[\textbf{б)}\ y = \frac{x^{2} - 25}{5 + |x|}\]

\[При\ x < - 5:\]

\[y = \frac{(x - 5)(x + 5)}{5 - x} = - x - 5.\]

\[При\ x > - 5:\]

\[y = \frac{(x - 5)(x + 5)}{5 + x} = x - 5.\]