Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 165
Задание 165
\[\boxed{\text{165\ (165).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\textbf{а)}\ \frac{2^{\backslash x} - \frac{a}{x}}{2^{\backslash x} + \frac{a}{x}} = \frac{2x - a}{x}\ :\frac{2x + a}{x} =\]
\[= \frac{2x - a}{x} \cdot \frac{x}{2x + a} = \frac{2x - a}{2x + a}\]
\[\textbf{б)}\ \frac{\frac{a - b}{c} + 3^{\backslash c}}{\frac{a + b}{c} - 1^{\backslash c}} =\]
\[= \frac{a - b + 3c}{c}\ :\frac{a + b - c}{c} =\]
\[= \frac{a - b + 3c}{c} \cdot \frac{c}{a + b - c} =\]
\[= \frac{a - b + 3c}{a + b - c}\]
\[\textbf{в)}\ \frac{\frac{1^{\backslash y}}{x} + \frac{1^{\backslash x}}{y}}{\frac{1^{\backslash y}}{x} - \frac{1^{\backslash x}}{y}} = \frac{y + x}{\text{xy}}\ :\frac{y - x}{\text{xy}} =\]
\[= \frac{y + x}{\text{xy}} \cdot \frac{\text{xy}}{y - x} = \frac{y + x}{y - x}\]
\[\textbf{г)}\ \frac{x - y}{\frac{x^{\backslash x}}{y} - \frac{y^{\backslash y}}{x}} =\]
\[= (x - y)\ :\frac{x^{2} - y^{2}}{\text{xy}} =\]
\[= (x - y) \cdot \frac{\text{xy}}{(x - y) \cdot (x + y)} =\]
\[= \frac{\text{xy}}{x + y}\]
\[\boxed{\text{165.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
Пояснение.
Решение.
\[\textbf{а)}\ \left( n + \frac{1}{n} \right)^{2} =\]
\[= n^{2} + 2n \cdot \frac{1}{n} + \frac{1}{n^{2}} =\]
\[= n^{2} + 2 + \frac{1}{n^{2}} =\]
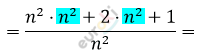
\[= \frac{n^{4} + 2n^{2} + 1}{n²}\]
\[\textbf{б)}\ \left( \frac{a^{\backslash a}}{b} - \frac{b^{\backslash b}}{a} \right)^{2} =\]
\[= \frac{a^{4} - 2a^{2}b^{2} + b^{4}}{a²b²}\]
\[\textbf{в)}\ \left( \frac{x}{y} + 1 \right)^{2} + \left( \frac{x}{y} - 1 \right)^{2} =\]
\[= \frac{x^{2}}{y^{2}} + 2\frac{x}{y} + 1 + \frac{x^{2}}{y^{2}} - 2\frac{x}{y} + 1 =\]
\[= \frac{2x^{2}}{y^{2}} + 2 = \frac{2x^{2} + 2y²}{y²}\]
\[\textbf{г)}\ \left( \frac{p}{q} + \frac{q}{p} \right)^{2} - \left( \frac{p}{q} - \frac{q}{p} \right)^{2} =\]
\[= \frac{p^{2}}{q^{2}} + \frac{2pq}{\text{pq}} + \frac{q^{2}}{p^{2}} - \frac{p^{2}}{q^{2}} + \frac{2pq}{\text{qp}} - \frac{q^{2}}{p^{2}} =\]
\[= \frac{2pq}{\text{qp}} + \frac{2pq}{\text{qp}} = \frac{4pq}{\text{pq}} = 4\]
