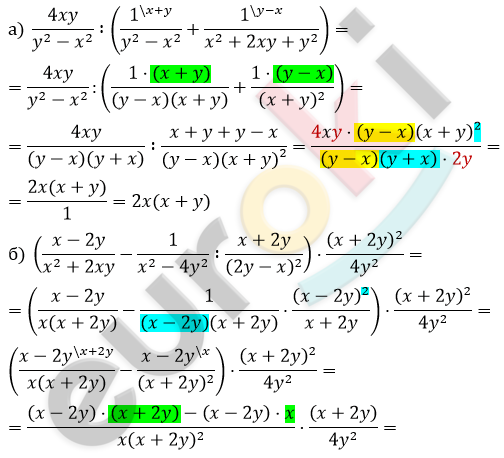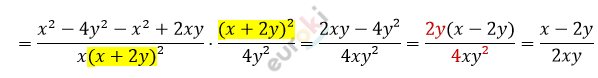Решебник по алгебре 8 класс Макарычев ФГОС Задание 157

 

\[\boxed{\text{157\ (157).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[a^{2} - 2a + 37 =\]

\[= a^{2} - 2a + 1 + 36 =\]

\[= (a - 1)^{2} + 36\]

\[(a - 1)^{2} \geq 0 - всегда\ \]

\[положительно,\ поэтому\ \]

\[(a - 1)^{2} + 36 > 0.\]

\[(a - 1)^{2} + 36 - принимает\ \]

\[наименьшее\ значение\ \]

\[при\ a = 1.\]

\[Ответ:при\ a = 1.\]

\[\boxed{\text{157.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Порядок действий в сложных примерах:

• сначала выполняем действия в скобках;

• потом слева направо умножение и деление;

• затем слева направо сложение и вычитание.

Дроби с разным знаменателем приводим к общему знаменателю.

Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй:

\[\frac{a}{b}\ :\frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a \cdot d}{b \cdot c}.\]

Вспомним формулы сокращения:

\[a^{2} - b^{2} = (a - b)(a + b);\]

\[a^{2} + 2ab + b^{2} = (a + b)^{2};\]

\[a^{2} - 2ab + b^{2} = (a - b)^{2}.\]

Решение.