Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 1111
Задание 1111
\[\boxed{\text{1111\ (1111).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
Решить уравнение – это значит найти все значения неизвестных, при которых оно обращается в верное числовое равенство, или доказать, что таких значений нет.
При решении уравнения используем:
1. Формулу квадрата разности:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:
\[\mathbf{(}\mathbf{a}\mathbf{-}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\mathbf{.}\]
2. Свойства уравнений:
1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2. Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.
Решение.
\[x^{2} - 2x + y^{2} - 4y + 5 = 0\]
\[\left( x^{2} - 2x + 1 \right) + \left( y^{2} - 4y + 4 \right) =\]
\[= 0\]
\[(x - 1)^{2} + (y - 2)^{2} = 0 \Longrightarrow\]
\[Ответ:x = 1,\ \ y = 2.\]
\[\boxed{\text{1111.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
\[\textbf{а)}\ \ \left( \frac{a + 1}{a^{2} + 1 - 2a} + \frac{1}{a - 1} \right) \cdot\]
\[\cdot \frac{a - 1}{a} - \frac{2}{a - 1} = 0\]
\[\left( \frac{a + 1}{(a - 1)^{2}} + \frac{1^{\backslash a - 1}}{a - 1} \right) \cdot \frac{a - 1}{a} -\]
\[- \frac{2}{a - 1} = 0\]
\[\frac{a + 1 + a - 1}{(a - 1)^{2}} \cdot \frac{a - 1}{a} -\]
\[- \frac{2}{a - 1} = 0\]
\[\frac{2a}{a(a - 1)} - \frac{2}{a - 1} = 0\]
\[\frac{2}{a - 1} - \frac{2}{a - 1} = 0\]
\[0 = 0.\]
\[Тождество\ доказано.\]
\[\textbf{б)}\ \left( \frac{1 + x}{x^{2} - xy} - \frac{1 - y}{y^{2} - xy} \right) \cdot\]
\[\cdot \frac{x^{2}y - y^{2}x}{x + y} = 1\]
\[\left( \frac{1 + x^{\backslash y}}{x(x - y)} + \frac{1 - y^{\backslash x}}{y(x - y)} \right) \cdot \ \]
\[\cdot \frac{x^{2}y - y^{2}x}{x + y} = 1\]
\[\frac{y + xy + x - xy}{\text{xy}(x - y)} \cdot \frac{\text{xy}(x - y)}{x + y} = 1\]
\[\frac{y + x}{x + y} = 1\]
\[1 = 1.\]
\[Тождество\ доказано.\]
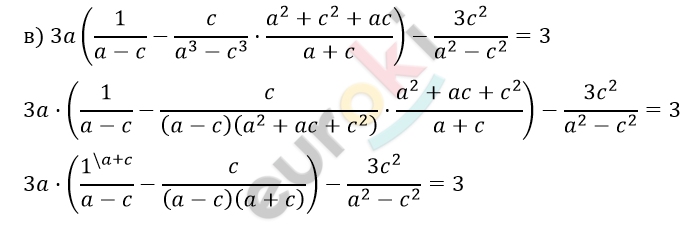
\[3a \cdot \frac{a + c - c}{a^{2} - c^{2}} - \frac{3c^{2}}{a^{2} - c^{2}} = 3\]
\[\frac{3a^{2} - 3c^{2}}{a^{2} - c^{2}} = 3\]
\[\frac{3 \cdot \left( a^{2} - c^{2} \right)}{a^{2} - c^{2}} = 3\]
\[3 = 3.\]
\[Тождество\ доказано.\]
