Решебник по алгебре 8 класс Макарычев ФГОС Задание 104
Задание 104



\[\boxed{\text{104\ (104).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Пусть\ туристы\ шли\ по\ шоссе\ \]
\[со\ скоростью\ \text{v\ }\frac{км}{ч};\]
\[(v - 2)\ \frac{км}{ч} - их\ скорость\ по\ \]
\[проселочной\ дороге.\]
\[Заполним\ таблицу:\]
| \[Скорость\] | \[Расстояние\] | \[Время\] | |
|---|---|---|---|
| \[Шоссе\] | \[v\] | \[s\] | \[\frac{s}{v}\] |
| \[Дорога\] | \[v - 2\] | \[2s\] | \[\frac{2s}{v - 2}\] |
Решение.
\[t = \frac{s^{\backslash v - 2}}{v} + \frac{2s^{\backslash v}}{v - 2}\]
\[t = \frac{sv - 2s + 2sv}{v(v - 2)} = \frac{3sv - 2s}{v(v - 2)} =\]
\[= \frac{s(3v - 2)}{v(v - 2)}.\]
\[При\ s = 10\ км;v = 6:\]
\[t = \frac{10 \cdot (3 \cdot 6 - 2)}{6 \cdot (6 - 2)} = \frac{10 \cdot 16}{6 \cdot 4} =\]
\[= \frac{5 \cdot 4}{3} = \frac{20}{3} = 6\frac{2}{3} = 6\frac{40}{60} =\]
\[= 6\ ч\ 40\ мин -\]
\[туристы\ затратили\ на\ весь\ \]
\[путь.\]
\[Ответ:6\ часов\ 40\ минут.\]

\[\boxed{\text{104.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
Пояснение.
Для того, чтобы сложить (вычесть) дроби с разными знаменателями, нужно привести их к общему знаменателю.
Решение.
\[\frac{1^{\backslash x + n + 1}}{x + n} - \frac{1^{\backslash x + n}}{x + n + 1} =\]
\[= \frac{1}{(x + n) \cdot (x + n + 1)}\]
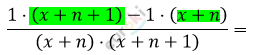
\[= \frac{1}{(x + n) \cdot (x + n + 1)}\]
\[\frac{x + n + 1 - x - n}{(x + n) \cdot (x + n + 1)} =\]
\[= \frac{1}{(x + n) \cdot (x + n + 1)}\]
\[\frac{1}{(x + n) \cdot (x + n + 1)} =\]
\[= \frac{1}{(x + n) \cdot (x + n + 1)}\]
\[Что\ и\ требовалось\ доказать.\]





