Решебник по алгебре 8 класс Макарычев ФГОС Задание 1003

 

\[\boxed{\text{1003\ (1003).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

аⁿ (а в n-ой степени) – число «n» называют показателем степени, а число «а» – основанием степени. Степень говорит нам о том, сколько раз следует умножить число «a» само на себя. Например, 3⁴=3*3*3*3=81.

Степень с отрицательным показателем – это дробь, числителем которой является единица, а знаменателем – данное число с положительным показателем:

\[\mathbf{a}^{\mathbf{- n}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{a}^{\mathbf{n}}}\mathbf{.}\]

При решении используем следующие правила:

1. При возведении произведения в степень каждый множитель возводят в степень и полученные результаты перемножают:

\(\mathbf{(}\mathbf{\text{ab}}\mathbf{)}^{\mathbf{n}}\mathbf{=}\mathbf{a}^{\mathbf{n}}\mathbf{\bullet}\mathbf{b}^{\mathbf{n}}\).

2. При возведении степени в степень (степень говорит нам о том, сколько раз следует умножить число само на себя. Например, 3⁴=3*3*3*3=81) показатели перемножаются, а основание остается прежним:

\[\mathbf{(}\mathbf{a}^{\mathbf{m}}\mathbf{)}^{\mathbf{n}}\mathbf{=}\mathbf{a}^{\mathbf{m \bullet n}}\mathbf{.}\]

3. Чтобы умножить число на дробь, нужно числитель умножить на это число, а знаменатель оставить без изменений:

\[\mathbf{a \bullet}\frac{\mathbf{b}}{\mathbf{c}}\mathbf{=}\frac{\mathbf{\text{ab}}}{\mathbf{c}}\mathbf{.}\]

4. Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй дроби, также умножить знаменатели. Первое произведение записать числителем, а второе – знаменателем:

\[\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\bullet}\frac{\mathbf{c}}{\mathbf{d}}\mathbf{=}\frac{\mathbf{\text{ac}}}{\mathbf{\text{bd}}}\mathbf{.}\]

5. Чтобы возвести дробь в отрицательную степень, нужно поменять местами числитель со знаменателем, а после возвести в степень уже без знака « – »:

\[\left( \frac{\mathbf{a}}{\mathbf{b}} \right)^{\mathbf{- n}}\mathbf{=}\left( \frac{\mathbf{b}}{\mathbf{a}} \right)^{\mathbf{n}}\mathbf{.}\]

6. Чтобы возвести дробь в степень, необходимо возвести в эту степень числитель и знаменатель:

\[\left( \frac{\mathbf{a}}{\mathbf{b}} \right)^{\mathbf{n}}\mathbf{=}\frac{\mathbf{a}^{\mathbf{n}}}{\mathbf{b}^{\mathbf{n}}}\mathbf{.}\]

Решение.

\[\textbf{а)}\ \left( 6a^{- 5}b \right)^{- 1} =\]

\[= 6^{- 1}\left( a^{- 5} \right)^{- 1}b^{- 1} =\]

\[= \frac{1}{6}a^{5} \cdot \frac{1}{b} = \frac{a^{5}}{6b}\]

\[\textbf{б)}\ \left( \frac{3}{4}a^{- 1}b^{- 3} \right)^{- 2} =\]

\[= \left( \frac{3}{4} \right)^{- 2} \cdot \left( a^{- 1} \right)^{- 2}\left( b^{- 3} \right)^{- 2} =\]

\[= \left( \frac{4}{3} \right)^{2}a^{2}b^{6} = \frac{16}{9}a^{2}b^{6}\]

\[\textbf{в)}\ \left( - 0,3x^{- 5}y^{4} \right)^{- 2} =\]

\[= ( - 0,3)^{- 2}\left( x^{- 5} \right)^{- 2}\left( y^{4} \right)^{- 2} =\]

\[= \left( - \frac{3}{10} \right)^{- 2}x^{10}y^{- 8} =\]

\[= \left( - \frac{10}{3} \right)^{2}x^{10}y^{- 8} = \frac{100x^{10}}{9y^{8}}\]

\[\textbf{г)}\ \left( \frac{7}{8}p^{- 6}q \right)^{- 1} =\]

\[= \left( \frac{7}{8} \right)^{- 1} \cdot \left( p^{- 6} \right)^{- 1} \cdot q^{- 1} = \frac{8p^{6}}{7q}\]

\[\boxed{\text{1003.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[велосипедиста\ по\ ровной\ \]

\[местности,\ тогда\]

\[(x - 5)\ \frac{км}{ч} - скорость\ \]

\[в\ \ гору.\]

\[\frac{60}{x}\ ч - по\ ровной\ местности;\ \ \]

\[\frac{20}{x - 5}\ ч - на\ путь\ в\ гору.\]

\[По\ условию\ \ \ на\ весь\ путь\ \]

\[затратил\ 6\ часов.\]

\[Составим\ уравнение:\]

\[\frac{60}{x} + \frac{20}{x - 5} = 6\]

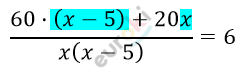
\[60x - 300 + 20x = 6x^{2} - 30x\]

\[6x² - 110x + 300 = 0\ \ \ \ \ |\ :2\]

\[3x^{2} - 55x + 150 = 0\]

\[D = 3025 - 1800 = 1225\]

\[x_{1,2} = \frac{+ 55 \pm \sqrt{1225}}{2 \cdot 3} = \frac{55 \pm 35}{6}\]

\[x_{1} = \frac{20}{6} < 5 - не\ может\ быть.\]

\[x_{2} = 15\ \left( \frac{км}{ч} \right) - скорость\ по\ \]

\[ровной\ местности.\]

\[15 - 5 = 10\ \left( \frac{км}{ч} \right) - скорость\]

\[\ в\ гору.\]

\[Ответ:15\ \frac{км}{ч}\ и\ 10\ \frac{км}{ч}\text{.\ }\]