Решебник по алгебре 8 класс Макарычев ФГОС Задание 100

 

\[\boxed{\text{100\ (100).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[ОДЗ:\]

\[x^{2} - 4 \neq 0\]

\[(x - 2)(x + 2) \neq 0\]

\[x \neq \pm 2.\]

\[\frac{x^{4} - 16}{x^{2} - 4} > 0\]

\[x^{2} + 4 > 0\]

\[Ответ:верно\ при\ любом\ x,\ \]

\[так\ как\ x^{2}\ всегда\ больше\ 0.\ \]

\[ОДЗ:\]

\[y^{2} - 1 \neq 0\]

\[(y - 1)(y + 1) \neq 0\]

\[y \neq \pm 1.\]

\[\frac{1 - y^{4}}{y^{2} - 1} < 0\]

\[- \frac{{1 - y}^{4}}{1 - y^{2}} < 0\]

\[Ответ:неравенство\ верно\ при\ \]

\[любом\ y,\ так\ как\ y^{2}\ всегда > 0,\]

\[а\ минус\ на\ плюс\ дает\ минус.\ \]

\[\boxed{\text{100.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Решение.

\[\textbf{а)}\ \frac{1^{\backslash a + 4b}}{a - 4b} - \frac{1^{\backslash a - 4b}}{a + 4b} - \frac{2a}{16b^{2} - a^{2}} =\]

\[= \frac{8b + 2a}{a^{2} - 16b^{2}} =\]

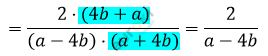
\[\textbf{б)}\ \frac{1}{2b - 2a} + \frac{1}{2b + 2a} + \frac{a^{2}}{a^{2}b - b^{3}} =\]

\[= \frac{b^{2} + ab + b^{2} - ab - 2a^{2}}{2b \cdot (b - a) \cdot (b + a)} =\]