Решебник по алгебре 8 класс Макарычев ФГОС Контрольные вопросы и задания к параграфу 12

\[\boxed{\text{12.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

\[\boxed{\text{1.\ }}\]

\[Множество,\ состоящее\ из\ всех\ \]

\[общих\ элементов\ этих\]

\[\ множеств -\]

\[пересечение\ множеств.\]

\[Множество,\ состоящее\ из\ всех\ \]

\[элементов,\ принадлежащих\]

\[\ хотя\]

\[бы\ одному\ из\ этих\ \ \]

\[множеств - объединение\]

\[\ множеств.\]

\[\boxed{\text{2.\ }}\]

\[\lbrack 1;2\rbrack - отрезок.\]

\[(1;2) - интервал.\]

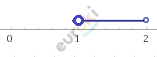
\[\lbrack 1;2),\ (1;2\rbrack - полуинтервал.\]

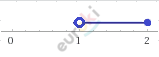
\[\lbrack 1;\ + \infty),\ ( - \infty;2\rbrack - числовой\ \]

\[луч.\]

\[(1;\ + \infty),\ ( - \infty;2) - открытый\]

\[\ числовой\ луч.\]

\[\boxed{\text{3.\ }}\]

\[Значение\ переменной,\ \]

\[которая\ обращает\ его\ в\]

\[\ верное\ неравенство -\]

\[это\ решение\ неравенства.\]

\[3x - 11 > 1\]

\[3x > 12\]

\[x > 4\]

\[При\ x = 5,\]

\[\ \ 5 > 4 \Longrightarrow является.\]

\[При\ x = 2,\]

\[\ \ 2 \ngtr 4 \Longrightarrow не\ является.\]

\[Решить\ неравенство - значит,\ \]

\[найти\ все\ значения,\ при\]

\[\ которых\ \]

\[оно\ верно.\]

\[\boxed{\text{4.\ }}\]

\[Решение\ системы\ \]

\[неравенств - значение\ \]

\[переменной,\ при\ которой\]

\[каждое\ неравенство\ верно.\]

\[\left\{ \begin{matrix} 2x + 1 > 3 \\ 3x < 10\ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\left\{ \begin{matrix} 2x > 2 \\ x < \frac{10}{3} \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\ \left\{ \begin{matrix} x > 1 \\ x < \frac{10}{3}\ \\ \end{matrix} \right.\ \Longrightarrow \ \frac{10}{3} \approx 3,3\]

\[x \in (1;3,3)\]

\[x = 3 \in (1;3,3) - да,\ является.\]

\[x = 5 \notin (1;3,3) - нет,\ \]

\[не\ является.\]

\[Решить\ систему - найти\ все\ \]

\[ее\ значения,\ при\ которых\ \]

\[все\ неравенства\]

\[верны.\]