Решебник по алгебре 8 класс Мерзляк контрольные работы КР-6. Квадратный трехчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений Вариант 4

Условие:

1. Разложите на множители квадратный трехчлен:

1) x^2+x-30

2) 2x^2-7x-9

2. Решите уравнение:

1) x^4+6x^2-27=0

2) (x^2-9)/(x+1)=8x/(x+1)

3. Сократите дробь (3a^2-11a-4)/(a^2-16).

4. Решите уравнение 4/(x^2-6x+9)-6/(x^2-9)=1/(x+3).

5. Катер прошёл 64 км против течения реки и 38 км по течению, затратив на путь по течению на 1 ч меньше, чем на путь против течения. Найдите собственную скорость катера, если скорость течения реки составляет 3 км/ч.

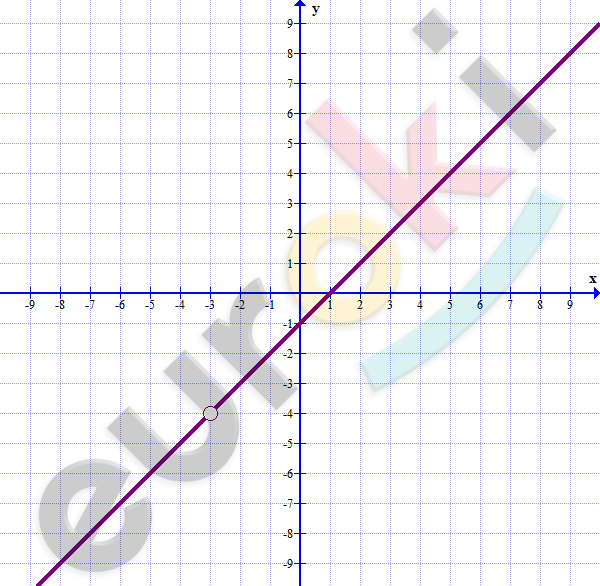
6. Постройте график функции y=(x^2+2x-3)/(x+3).

Решение:

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[1)\ x^{2} + x - 30\]

\[x_{1} + x_{2} = - 1;\ \ x_{1} \cdot x_{2} = - 30\]

\[x_{1} = - 6;\ \ x_{2} = 5\]

\[x^{2} + x - 30 = (x + 6)(x - 5).\]

\[2)\ 2x^{2} - 7x - 9\]

\[D = 49 + 72 = 121\]

\[x_{1} = \frac{7 + 11}{4} = \frac{18}{4} = \frac{9}{2};\]

\[x_{2} = \frac{7 - 11}{4} = - \frac{4}{4} = - 1.\]

\[2x^{2} - 7x - 9 =\]

\[= 2 \cdot (x + 1)\left( x - \frac{9}{2} \right) =\]

\[= (x + 1)(2x - 9).\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[1)\ x^{4} + 6x^{2} - 27 = 0\]

\[Пусть\ x^{2} = t \geq 0:\]

\[t^{2} + 6t - 27 = 0\]

\[t_{1} + t_{2} = - 6;\ \ \ t_{1} \cdot t_{2} = - 27\]

\[t_{1} = - 9\ (не\ подходит);\ \ \]

\[t_{2} = 3.\]

\[x^{2} = 3\]

\[x = \pm \sqrt{3}.\]

\[Ответ:x = \pm \sqrt{3}.\]

\[2)\ \frac{x^{2} - 9}{x + 1} = \frac{8x}{x + 1};\ \ \ \ \ x \neq - 1\]

\[x^{2} - 9 = 8x\]

\[x^{2} - 8x - 9 = 0\]

\[x_{1} + x_{2} = 8;\ \ \ x_{1} \cdot x_{2} = - 9\]

\[x_{1} = 9;\ \ \ \]

\[x_{2} = - 1\ (не\ подходит).\]

\[Ответ:\ \ x = 9.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[\frac{3a^{2} - 11a - 4}{a^{2} - 16} =\]

\[= \frac{(3a + 1)(a - 4)}{(a - 4)(a + 4)} = \frac{3a + 1}{a + 4}\]

\[3a^{2} - 11a - 4 =\]

\[= 3 \cdot \left( a + \frac{1}{3} \right)(a - 4) =\]

\[= (3a + 1)(a - 4)\]

\[D = 121 + 48 = 169\]

\[a_{1} = \frac{11 + 13}{6} = 4;\]

\[a_{2} = \frac{11 - 13}{6} = - \frac{2}{6} = - \frac{1}{3}.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\frac{4}{x^{2} - 6x + 9} - \frac{6}{x^{2} - 9} = \frac{1}{x + 3}\]

\[\frac{4}{(x - 3)^{2}} - \frac{6}{(x - 3)(x + 3)} - \frac{1}{x + 3} = 0\]

\[ОДЗ:\ \ x \neq 3;\ \ x \neq - 3.\]

\[4 \cdot (x + 3) - 6 \cdot (x - 3) - (x - 3)^{2} = 0\]

\[4x + 12 - 6x + 18 - x^{2} + 6x - 9 = 0\]

\[- x^{2} + 4x + 21 = 0\]

\[x^{2} - 4x - 21 = 0\]

\[x_{1} + x_{2} = 4;\ \ \ x_{1} \cdot x_{2} = - 21\]

\[x_{1} = 7;\ \ \ \]

\[x_{2} = - 3\ (не\ подходит).\]

\[Ответ:x = 7.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[Пусть\ \text{x\ }\frac{км}{ч} - собственная\ \]

\[скорость\ катера;тогда\ \]

\[(x + 2)\ \frac{км}{ч} - скорость\ по\ \]

\[течению;\]

\[(x - 2)\ \frac{км}{ч} - скорость\ \]

\[против\ течения;\]

\[\frac{38}{x + 3}\ \ ч - шел\ по\ течению;\]

\[\frac{64}{x - 3}\ ч - шел\ против\ течения.\]

\[Составим\ уравнение:\]

\[\frac{64}{x - 3} - \frac{38}{x + 3} = 1;\ \ \ \ x \neq \pm 3\]

\[64 \cdot (x + 3) - 38 \cdot (x - 3) = x^{2} - 9\]

\[64x + 192 - 38x + 114 = x^{2} - 9\]

\[x^{2} - 26x - 9 - 306 = 0\]

\[x^{2} - 26x - 315 = 0\]

\[x_{1} + x_{2} = 26;\ \ \ x_{1} \cdot x_{2} = - 315\]

\[x_{1} = 22\ \left( \frac{км}{ч} \right) - собственная\ \]

\[скорость\ катера.\]

\[x_{2} = - 9\ (не\ подходит).\]

\[Ответ:22\ \frac{км}{ч}.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[y = \frac{x^{2} + 2x - 3}{x + 3} =\]

\[= \frac{(x + 3)(x - 1)}{x + 3} = x - 1\]

\[x^{2} + 2x - 3 = (x + 3)(x - 1).\]

\[x_{1} + x_{2} = - 2;\ \ \ x_{1} \cdot x_{2} = - 3\]

\[x_{1} = - 3;\ \ x_{2} = 1.\]

\[y = x - 1;\ \ где\ x \neq - 3\]

## КР-7. Обобщение и систематизация знаний учащихся