Решебник по алгебре 8 класс Мерзляк контрольные работы КР-7. Обобщение и систематизация знаний учащихся Вариант 1

Условие:

1. Сократите дробь (21x^8 y^12)/(14x^4 y^24).

2. Представьте в виде степени выражение (a^(-2) )^6:a^(-15).

3. Упростите выражение √16a-√64a+√100a.

4. При каких значениях переменной имеет смысл выражение (x-1)/(2x^2-5x+2).

5. Докажите тождество

3/(2a-3)-(8a^3-18a)/(4a^2+9)·(2a/(4a^2-12a+9)-3/(4a^2-9))=-1.

6. Тракторист должен был за определённое время вспахать поле площадью 180 га. Однако ежедневно он вспахивал на 2 га больше, чем планировал, и закончил работу на день раньше срока. За сколько дней тракторист вспахал поле?

7. Докажите, что при любом значении p уравнение x^2+ px + p – 1 = 0 имеет хотя бы один корень.

8. Постройте график функции

Решение:

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[\frac{21x^{8}y^{12}}{14x^{4}y^{24}} = \frac{3x^{4}}{2y^{12}}\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[\left( a^{- 2} \right)^{6}\ :a^{- 15} = a^{- 12}\ :a^{- 15} = a^{3}.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[\sqrt{16a} - \sqrt{64a} + \sqrt{100a} =\]

\[= 4\sqrt{a} - 8\sqrt{a} + 10\sqrt{a} = 6\sqrt{a}.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\frac{x - 1}{2x^{2} - 5x + 2}\]

\[2x^{2} - 5x + 2 \neq 0\]

\[D = 25 - 16 = 9\]

\[x_{1} = \frac{5 + 3}{4} = 2;\ \ \]

\[x_{2} = \frac{5 - 3}{4} = 0,5.\]

\[D(y) = ( - \infty;0,5) \cup (0,5;2) \cup (2; + \infty).\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[1)\frac{2a^{\backslash 2a + 3}}{(2a - 3)^{2}} - \frac{3^{\backslash 2a - 3}}{(2a - 3)(2a + 3)} =\]

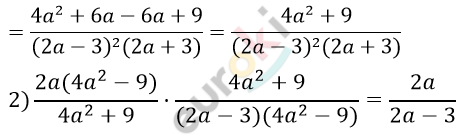
\[3)\frac{3}{2a - 3} - \frac{2a}{2a - 3} = \frac{3 - 2a}{2a - 3} = - 1\]

\[- 1 = - 1\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[Пусть\ x\ га\ в\ день - планировал\ \]

\[вспахивать\ тракторист,\ тогда\ \]

\[\left( \frac{180}{x} \right)\ дней - планировал\ он\ \]

\[потратить\ на\ вспахивание\ \]

\[поля.\]

\[(x + 2)\ га\ в\ день - стал\ пахать\ \]

\[тракторист,\ \]

\[\left( \frac{180}{x + 2} \right)\ дней - будет\ пахать\ \]

\[все\ поле.\]

\[По\ условию\ известно,\ что\ он\ \ \]

\[закончил\ работу\ на\ 1\ день\ \]

\[раньше\ срока.\]

\[Составляем\ уравнение:\]

\[\frac{180}{x} - \frac{180}{x + 2} = 1\]

\[180 \cdot (x + 2) - 180 \cdot x - x(x + 2) = 0\]

\[180x + 360 - 180x - x^{2} - 2x = 0\]

\[- x^{2} - 2x + 360 = 0\]

\[x^{2} + 2x - 360 = 0\]

\[x_{1} + x_{2} = - 2;\ \ \ x_{1}x_{2} = - 360,\ \ \]

\[x_{1} = - 20\ (не\ удовлетворяет),\ \ \]

\[x_{2} = 18\ (га\ в\ день) - \ \]

\[планировал\ вспахивать\ \]

\[тракторист.\]

\[\frac{180}{18 + 2} = \frac{180}{20} = 9\ (дней) - \ \]

\[ушло\ у\ тракториста\ на\ \]

\[вспахивание\ поля.\]

\[Ответ:9\ дней.\]

\[\boxed{\mathbf{7}\mathbf{.}\mathbf{\ }}\]

\[x^{2} + px + p - 1 = 0\]

\[Уравнение\ имеет\ хотя\ бы\ \ \]

\[один\ корень\ при\ D \geq 0.\]

\[D = p^{2} - 4 \cdot (p - 1) =\]

\[= p^{2} - 4p + 4 = (p - 2)^{2} \geq 0\ \]

\[при\ всех\ значениях\ \text{p.}\]

\[Что\ и\ требовалось\ доказать.\]

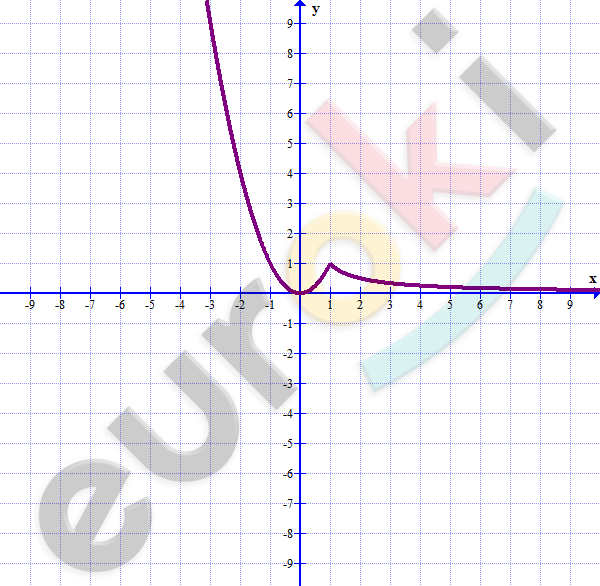
\[\boxed{\mathbf{8}\mathbf{.}\mathbf{\ }}\]

\[y = \left\{ \begin{matrix} x^{2};\ \ если\ x \leq 1 \\ \frac{1}{x};\ \ \ если\ x > 1 \\ \end{matrix} \right.\ \]