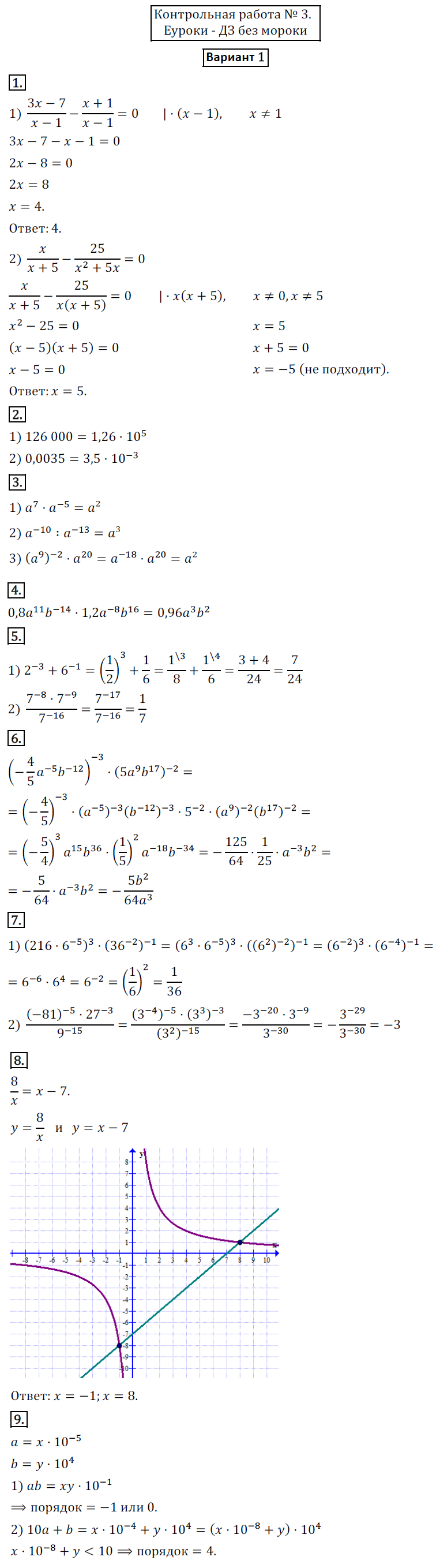Решебник по алгебре 8 класс Мерзляк дидактические материалы КР-3. Рациональные уравнения. Степень с целым отрицательным показателем | Номер Вариант 1

Условие:

1. Решите уравнение:

1) (3x-7)/(x-1)-(x+1)/(x-1)=0;

2) x/(x+5)-25/(x^2+5x)=0.

2. Запишите в стандартном виде число:

1) 126 000;

2) 0,0035.

3. Представьте в виде степени с основанием a выражение:

1) a^7*a^(-5);

2) a^(-10)∶a^(-13);

3) (a^9)^(-2)*a^20.

4. Упростите выражение 0,8a^11b^(-14)*1,2a^(-8)b^16.

5. Найдите значение выражения:

1) 2^(-3)+6^(-1);

2) (7^(-8)*7^(-9))/7^(-16) .

6. Преобразуйте выражение (-4/5a^(-5)b^(-12))^(-3)*(5a^9b^17)^(-2) так, чтобы оно не содержало степеней с отрицательными показателями.

7. Вычислите:

1) (216*6^(-5))^3*(36^(-2))^(-1);

2) ((-81)^(-5)*27^(-3))/9^(-15).

8. Решите графически уравнение 8/x=x-7.

9. Порядок числа a равен -5, а порядок числа b равен 4. Каким может быть порядок значения выражения:

1) ab;

2) 10a+b?