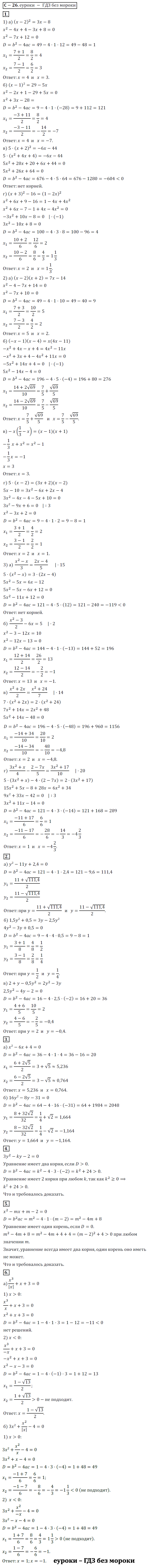Решебник по алгебре 8 класс Жохов дидактические материалы С-26(26). Решение квадратных уравнений (продолжение) | Номер Вариант 1

Условие:

1. Найдите корни уравнения:

1) а) (x-2)^2=3x-8;

2) а) (x-2)(x+2)=7x-14;

3) а) (x^2-x)/3=(2x-4)/5.

2. При каких значениях y:

а) значение многочлена y^2-11y+2,4 равно нулю;

б) равны значения двучленов 1,5y^2+0,5 и 3y-2,5y^2;

в) трёхчлен 2+y-0,5y^2 равен двучлену 2y^2-3y?

3. Найдите корни уравнения и укажите их приближенные значения в виде десятичных дробей с точностью до 0,001:

а) x^2-6x+4=0.

4. Докажите, что при любом значении k уравнение 3y-ky-2=0 имеет два корня.

5. Докажите, что не существует такого значения m, при котором уравнение

x^2-mx+m-2=0 имело бы один корень.

6. Решите уравнение:

а) x^3/|x|+x+3=0.