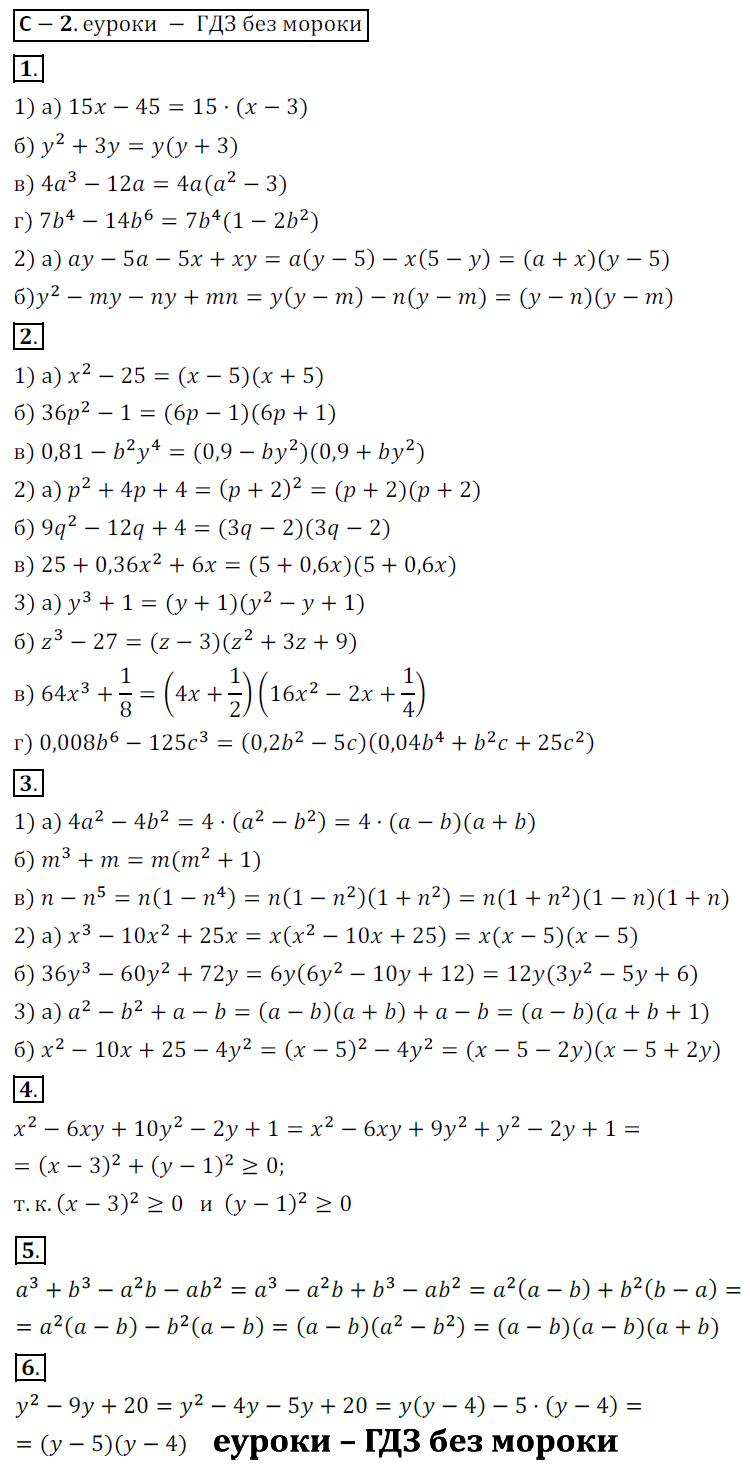Решебник по алгебре 8 класс Жохов дидактические материалы С-2(2). Разложение на множители | Номер Вариант 2

Условие:

1. Представьте многочлен в виде произведения

1) а) 15x-45

б) y^2+3y

в) 4a^3-12a

г) 7b^4-14b^6

2) а) ay-5a-5x+xy

б) y^2-my-ny+mn

2. Разложите на множители

1) а) x^2-25

б) 36p^2-1

в) 0,81-b^2*y^4

2) а) p^2+4p+4

б) 9q^2-12q+4

в) 25+0,36x^2+6x

3) а) y^3+1

б) z^3-27

в) 64x^3+1/8

г) 0,008b^6-12c^3

3. Разложите на множители

1) а) 4a^2-4b^2

б) m^3+m

в) n-n^5

2) а) x^3-10x^2+25x

б) 36y^3-60y^2+72y

3) а) a^2-b^2+a-b

б) x^2-10x+25-4y^2

4. Докажите, что многочлен x^2-6xy+10y^2-2y+1 при любых значениях х и у принимает неотрицательные значения.

5. Разложите на множители многочлен a^3+b^3-a^2b-ab^2.

6. Представьте трехчлен y^2-9y+20 в виде произведения двух двучленов.