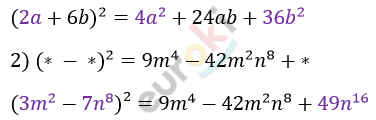Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 7 класс Мерзляк ФГОС Задание 703
Задание 703
\[\boxed{\text{703\ (703).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[1)\ a + a² + a³ + a^{4} + \ldots + a^{100}\]
\[при\ a = 1 \Longrightarrow\]
\[\Longrightarrow 1 + 1 + 1 + 1 + \ldots + 1^{100} =\]
\[= 100\]
\[2)\ a + a² + a³ + a^{4} + \ldots + a^{98} + a^{99}\]
\[при\ a = 1 \Longrightarrow\]
\[\Longrightarrow 1 + 1 + 1 + \ldots + 1^{99} = 99\]
\[при\ a = - 1 \Longrightarrow\]
\[\Longrightarrow - 1 + 1 - 1 + 1 + \ldots + 1^{98} - 1^{99} =\]
\[= - 1\]
\[3)\ aa^{2}a^{3}a^{4}\ldots a^{99}a^{100}\]
\[при\ a = 1 \Longrightarrow\]
\[\Longrightarrow 1 \cdot 1 \cdot 1 \cdot 1\ldots \cdot 1 \cdot 1 = 1\]
\[при\ a = - 1 \Longrightarrow\]
\[\Longrightarrow - 1 \cdot 1 \cdot ( - 1) \cdot 1\ldots \cdot ( - 1)^{99} \cdot 1 =\]
\[= 1\]
\[4)\ aa^{2}a^{3}a^{4}\ldots a^{98}a^{99}\]
\[при\ a = 1 \Longrightarrow\]
\[\Longrightarrow 1 \cdot 1 \cdot 1 \cdot 1\ldots \cdot 1 \cdot 1 = 1\]
\[при\ a = - 1 \Longrightarrow\]
\[\Longrightarrow - 1 \cdot 1 \cdot ( - 1) \cdot 1\ldots \cdot 1 \cdot ( - 1) =\]
\[= - 1\]
\[\boxed{\text{703.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Одночлены,\ на\ которые\ мы\ \]
\[заменили\ звездочки,\ \]
\[выделены\ цветом.\]
\[1)\ (*\ + 6b)^{2} = \ *\ + \ 24ab + \ *\]
