Решебник по алгебре 7 класс Мерзляк ФГОС Задание 469

 

\[\boxed{\text{469\ (469).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ a - число\ десятков;b -\]

\[число\ единиц\ в\ двузначном\ \]

\[числе;\]

\[(10a + b) - искомое\ число.\]

\[Получаем:\]

\[10a + b = (a + 1) \cdot (b + 1)\]

\[10a + b = ab + a + b + 1\]

\[10a + b - ab - a - b - z = 0\]

\[9a - 1 = ab\]

\[9a - ab = 1\]

\[a(9 - b) = 1\]

\[a = 1;\ \ \ \ 9 - b = 1\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b = 8.\]

\[Искомое\ число:\ \ \ 18.\]

\(Ответ:18.\ \)

\[\boxed{\text{469.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ a \cdot (a + b) - b \cdot (a - b) =\]

\[= a^{2} + b^{2}\]

\[Упростим\ левую\ часть\ \]

\[равенства:\]

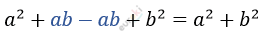
\[a^{2} + b^{2} = a^{2} + b^{2}.\]

\[Тождество\ доказано.\]

\[2)\ b \cdot (a - b) + b \cdot (b + c) =\]

\[= b \cdot (a + b) - b \cdot (b - c)\]

\[Упростим\ обе\ части\ \]

\[равенства:\]

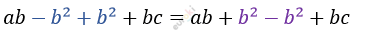
\[ab + bc = ab + bc.\ \]

\[Тождество\ доказано.\]