Решебник по алгебре 7 класс Мерзляк ФГОС Задание 363

 

\[\boxed{\text{363\ (363).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Упростим\ левую\ часть\ \]

\[равенства:\]

\[abc = abc.\]

\[Тождество\ доказано.\]

\[Упростим\ левую\ часть\ \]

\[равенства:\]

\[a^{2} = a^{2}.\]

\[Тождество\ доказано.\]

\[3)\ a \cdot (a + 2b) + b \cdot (a + b) =\]

\[= b \cdot (2a + b) + a \cdot (a + b)\]

\[Упростим\ левую\ и\ правую\ \]

\[части\ равенства:\]

\[a^{2} + 2ab + ab + b^{2} =\]

\[= 2ab + b^{2} + a^{2} + ab\]

\[a^{2} + b^{2} + 3ab = a^{2} + b^{2} + 3ab.\]

\[Тождество\ доказано.\]

\[Упростим\ левую\ и\ правую\ \]

\[части\ равенства:\]

\[ac - bc = ac - bc.\ \]

\[Тождество\ доказано.\]

\[\boxed{\text{363.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ 2\frac{5}{6}a^{n + 2}b^{m + 3} \cdot \frac{9}{17}a^{5n - 4}b^{2m - 1} =\]

\[= \frac{17 \cdot 9}{6 \cdot 17}a^{n + 2 + 5n - 4}b^{m + 3 + 2m - 1} =\]

\[= 1,5a^{6n - 2}b^{3m + 2}\]

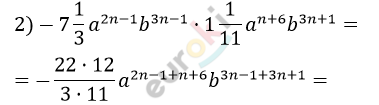
\[= - 8a^{3n + 5}b^{6n}\]