Решебник по алгебре 7 класс Мерзляк ФГОС Задание 341

 

\[\boxed{\text{341\ (341).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[= 5n + 10 = 5 \cdot (n + 2) -\]

\[делится\ на\ 5.\]

\[2)\ 2n + (2n + 2) + (2n + 4) =\]

\[= 2n + 2n + 2 + 2n + 4 =\]

\[= 6n + 6 =\]

\[= 6 \cdot (n + 1) - делится\ на\ 6.\]

\[= 8 \cdot (n + 2) - делится\ на\ 8.\]

\[= 4n + 6 =\]

\[= 4 \cdot (n + 1) + 2 - делится\ на\ \]

\[4\ и\ остаток\ 2.\]

\[= 5n + 10 + n + 5 =\]

\[= 6n + 15 = 6n + 12 + 3 =\]

\[= 6 \cdot (n + 2) + 3 - делится\ на\ \]

\[6\ и\ остаток\ 3.\ \]

\[\boxed{\text{341.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\overline{\text{abcabc}} - шестизначное\ число.\]

\[\overline{\text{abcabc}} =\]

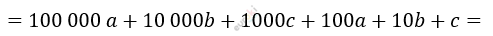
\[= 100\ 100a + 10\ 010b + 1001c =\]

\[= 1001 \cdot (10a + 10b + c)\]

\[Так\ как\ число\ 1001\ делится\ на\ \]

\[7,\ на\ 11\ и\ на\ 13,\ то\ и\ все\ \]

\[шестизначное\ число\ будет\ \]

\[делиться\ на\ данные\ числа.\]

\[Пусть\ наше\ число\ 345\ 345,\ в\ \]

\[котором\ первые\ три\ цифры\ \]

\[равны\ трем\ последним\ \]

\[цифрам.\ На\ 7,\ 11\ и\ 13\ делятся\ \]

\[числа,\ у\ которых\ разность\ \]

\[между\ числом,\ выраженным\ \]

\[тремя\ последними\ цифрами\ и\ \]

\[числом,выраженным\ \]

\[остальными\ цифрами,\ делится\ \]

\[на\ 7,\ 11\ и\ 13.\]

\[Тогда:\ 345 - 345 =\]

\[= 0 \Longrightarrow делится\ на\ 11,13\ и\ 7.\]