Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 7 класс Мерзляк ФГОС Задание 124
Задание 124
\[\boxed{\text{124\ (}\text{н}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\textbf{а)}\ нет:\ \ по\ схеме\ видно,\ что\ \]
\[города\ С,М,О,К\ не\ могут\ \]
\[иметь\ дороги\ к\ городам\ И,У,П,\]
\[Т.\]
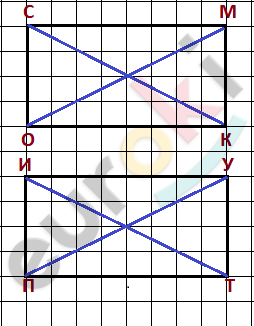
\[Следовательно,\ нельзя\ \]
\[утверждать,\ что\ из\ любого\ \]
\[города\ можно\ проехать\ в\ \]
\[любой\ другой\ город,\ если\ из\ \]
\[каждого\ выходит\ не\ менее\]
\[трех\ дорог.\]
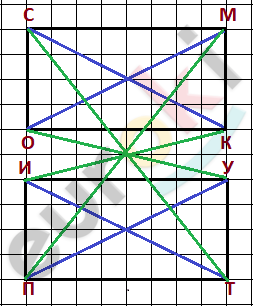
\[\textbf{б)}\ Пойдем\ от\ обратного:если\ \]
\[бы\ каждый\ город\ этого\ \]
\[региона\ был\ связан\ только\ с\ \]
\[четырьми\ другими\ и\ никак\ не\ \]
\[был\ бы\ связан\ с\ остальными,\ \]
\[то\ в\ регионе\ должно\ было\ бы\ \]
\[быть\ как\ минимум\ 10\ городов.\ \]
\[Но\ так\ как\ у\ нас\ городов\ 8,\ то\ \]
\[получаем\ противоречие.\]
\[Значит,\ из\ любого\ города\ \]
\[можно\ проехать\ в\ любой\ \]
\[другой\ город\ этого\ региона.\]
\[\boxed{\text{124\ (}\text{с}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[В\ I\ растворе\ соли\ 0,25;\ \ \ воды\ \]
\[0,75;\]
\[Во\ \text{II}\ растворе\ соли\ 0,4;\ \ \ воды\ \]
\[0,6;\]
\[В\ \text{III}\ растворе\ соли\ 0,34;\ \ \ воды\ \]
\[0,66.\]
\[50 \cdot 0,34 = 17\ (кг) - соли\ в\ \]
\[третьем\ растворе.\]
\[50 \cdot 0,66 = 33\ (кг) - воды\ в\ \]
\[третьем\ растворе.\]
\[Пусть\ x_{1}\ кг\ соли\ во\ втором\ \]
\[растворе,\ то\ \left( 17 - x_{1} \right)\ кг -\]
\[соли\ в\ первом\ растворе.\]
\[Составим\ уравнение:\]
\[0,4x_{1} + 0,25 \cdot \left( 17 - x_{1} \right) =\]
\[= 0,34 \cdot 17\]
\[0,4x_{1} + 4,25 - 0,25x_{1} = 5,78\]
\[0,15x_{1} = 5,78 - 4,25\]
\[0,15x_{1} = 1,53\]
\[x_{1} = 10,2\ (кг) - соли\ во\ втором\]
\[\ растворе.\]
\[17 - 10,2 = 6,8\ (кг) - соли\ в\ \]
\[первом\ растворе.\]
\[Пусть\ x_{2}\ кг\ воды\ в\ первом\ \]
\[растворе,\ то\ \left( 33 - x_{2} \right)\ кг\ воды\ \]
\[во\ втором\ растворе.\]
\[Составим\ уравнение:\]
\[0,75x_{2} + 0,6 \cdot \left( 33 - x_{2} \right) =\]
\[= 0,66 \cdot 33\]
\[0,75x_{2} + 19,8 - 0,6x_{2} = 21,78\]
\[0,15x_{2} = 21,78 - 19,8\]
\[0,15x_{2} = 1,98\]
\[x_{2} = 13,2\ (кг) - воды\ в\ первом\ \]
\[растворе.\]
\[33 - 13,2 = 19,8\ (кг) - воды\ \]
\[во\ втором\ растворе.\]
\[13,2 + 6,8 = 20\ (кг) - масса\ \]
\[первого\ раствора.\]
\[10,2 + 19,8 = 30\ (кг) - масса\ \]
\[второго\ раствора.\]
\[Пусть\ \text{x\ }кг\ надо\ взять\ первого\ \]
\[раствора,\ тогда\ (50 - x)\ кг\ \]
\[надо\ взять\ второго\ раствора.\]
\[0,24\text{x\ }кг - масса\ соли\ в\ первом\ \]
\[растворе;\]
\[0,4 \cdot (50 - x)\ кг - масса\ соли\ \]
\[во\ втором\ растворе.\]
\[В\ итоговом\ растворе\ масса\ \]
\[соли\ равна\ 0,34 \cdot 50.\]
\[Составим\ уравнение:\]
\[0,25x + 0,4 \cdot (50 - x) =\]
\[= 0,34 \cdot 50\]
\[0,25x + 20 - 0,4x = 17\]
\[- 0,15x = 17 - 20\]
\[- 0,15x = - 3\]
\[x = 3\ :0,15 = 300\ :15 =\]
\[= 20\ (кг) - первого\ раствора\]
\[\ нужно\ взять.\]
\[50 - 20 = 30\ (кг) - второго\]
\[\ раствора\ надо\ взять.\]
\[Ответ:20\ кг;30\ кг.\ \]
\[\boxed{\text{124.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
Пояснение.
Решение.
\[1)\ |x| + 6 = 13\]
\[|x| = 13 - 6\]
\[|x| = 7\]
\[x = \pm 7\]
\[Ответ:x = \pm 7.\]
\[2)\ |x| - 7 = - 12\]
\[|x| = - 12 + 7\]
\[|x| = - 5\]
\[Ответ:нет\ корней.\]
\[3)\ 7 \cdot |x| - 3 = 0\]
\[7 \cdot |x| = 3\]
\[|x| = \frac{3}{7}\]
\[x = \pm \frac{3}{7}\]
\[Ответ:x = \pm \frac{3}{7}.\]
\[4)\ |x - 5| = 4\]
\[Ответ:x = 1;9.\]
\[5)\ |9 + x| = 0\]
\[9 + x = 0\]
\[x = - 9\]
\[Ответ:x = - 9.\]
\[6)\ |x - 4| = - 2\]
\[Модуль\ не\ может\ быть\ \]
\[отрицательным\ числом.\]
\[Ответ:нет\ корней.\]
\[7)\ |3x + 4| = 2\]
\[Ответ:\ x = - 2; - \frac{2}{3}.\]
\[8)\ |2x + 1| + 13 = 14\]
\[|2x + 1| = 14 - 13\]
\[|2x + 1| = 1\]
\[2x + 1 = - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2x + 1 = 1\]
\[2x = - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2x = 0\]
\[x = - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = 0\]
\[Ответ:x = 0;\ \ 1.\]
\[9)\ \left| |x| - 3 \right| = 5\]
\[|x| - 3 = - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ |x| - 3 = 5\]
\[|x| = - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ |x| = 8\]
\[корней\ нет.\ \ \ \ \ \ \ \ \ \ \ \ \ \ x = \pm 8\]
\[Ответ:x = \pm 8.\]
