Решебник по алгебре 7 класс Макарычев ФГОС Задание 665

 

\[\boxed{\text{665.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Алгоритм решения задач с помощью уравнений:

• обозначить неизвестное число буквой (чаще всего x);

• составить уравнение по условию задачи;

• решить уравнение;

• записать пояснение.

Концентрация раствора – это число, которое показывает сколько граммов (мл) сухого вещества содержится в 100 мл раствора.

Чтобы ее найти, нужно массу растворенного вещества разделить на массу раствора.

Решение.

\[Пусть\ в\ сплаве\ первоначально\ \]

\[было\ \text{x\ }кг\ олова.\ Тогда\ \]

\[изначальное\ содержание\ олова\ \]

\[в\ сплаве\ было\ \frac{x}{16}\text{.\ }\]

\[После\ добавления\ 2\ кг\ олова,\]

\[содержание\ стало\ равным\ \ \]

\[\frac{x + 2}{18}.\ По\ условию\ задачи,\ \]

\[оно\ повысилось\]

\[на\ 5\% = \frac{5}{100} = 0,05.\]

\[Составим\ и\ решим\ уравнение:\]

\[16 \cdot (x + 2) = 18x + 0,05 \cdot 288\]

\[16x + 32 - 18x = 14,4\]

\[- 2x = 14,4 - 32\]

\[- 2x = - 17,6\]

\[x = - 17,6\ :( - 2)\]

\[x = 8,8\ (кг) - олова\ было\ \]

\[в\ сплаве\ первоначально.\]

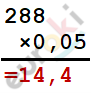
\[Ответ:8,8\ кг\ олова\ было\ \]

\[первоначально\ в\ сплаве.\]

\[\boxed{\text{665\ (665).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ 7^{8} - 7^{7} + 7^{6} =\]

\[= 7^{6} \cdot \left( 7^{2} - 7 + 1 \right) =\]

\[= 7^{6} \cdot (49 - 6) =\]

\[= 7^{6} \cdot 43 \Longrightarrow делится\ на\ 43;\]

\[\textbf{б)}2^{13} - 2^{10} - 2^{9} =\]

\[= 2^{9} \cdot \left( 2^{4} - 2 - 1 \right) =\]

\[= 2^{9} \cdot (16 - 3) =\]

\[= 2^{9} \cdot 13 \Longrightarrow делится\ на\ 13;\]

\[\textbf{в)}\ 27^{4} - 9^{5} + 3^{9} =\]

\[= 3^{12} - 3^{10} + 3^{9} =\]

\[= 3^{9} \cdot \left( 3^{3} - 3 + 1 \right) =\]

\[= 3^{9} \cdot (27 - 2) =\]

\[= 3^{9} \cdot 25 \Longrightarrow делится\ \ на\ 25;\]

\[\textbf{г)}\ 16^{4} - 2^{13} - 4^{5} =\]

\[= 2^{16} - 2^{13} - 2^{10} =\]

\[= 2^{10} \cdot \left( 2^{6} - 2^{3} - 1 \right) =\]

\[= 2^{10} \cdot (64 - 8 - 1) = 2^{10} \cdot 55 =\]

\[= 2^{9} \cdot 110 \Longrightarrow делится\ на\ 110.\]