Решебник по алгебре 7 класс Макарычев ФГОС Задание 556

 

\[\boxed{\text{556.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Формула для нахождения объема шара через радиус:

.

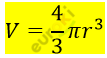Решение.

\[Если\ радиус\ увеличить\ \]

\[в\ 2\ раза,\ то:\ \]

\[V = \frac{4}{3}\pi \cdot (2r)^{3} = \frac{4}{3}\pi \cdot 8r^{3} =\]

\[= 8 \cdot \left( \frac{4}{3}\pi r^{3} \right)\]

\[то\ есть,\ объем\ увеличится\ \]

\[в\ 8\ раз.\]

\[Если\ радиус\ увеличить\ \]

\[в\ 4\ раза,\ то:\ \]

\[V = \frac{4}{3}\pi \cdot (4r)^{3} = \frac{4}{3}\pi \cdot 64r^{3} =\]

\[= 64 \cdot \left( \frac{4}{3}\pi r^{3} \right)\ \]

\[то\ есть,\ объем\ увеличится\ \]

\[в\ 64\ раза.\]

\[\boxed{\text{556\ (556).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ 100x^{5}y^{3} = 20x^{4}y \cdot 5xy^{2}\]

\[\textbf{б)} - 30x^{4}y^{5} = 20x^{4}y \cdot ( - 1,5y^{4})\]

\[\textbf{в)} - 4x^{16}y = 20x^{4}y \cdot \left( - 0,2x^{12} \right)\]

\[\textbf{г)}\ x^{10}y^{2} = 20x^{4}y \cdot \frac{1}{20}x^{6}y\]

\[\textbf{д)}\ 5x^{8}y = 20x^{4}y \cdot \frac{1}{4}x^{4}\]

\[\textbf{е)} - x^{4}y^{2} = 20x^{4}y \cdot \left( - \frac{1}{20}y \right)\]