Решебник по алгебре 7 класс Макарычев ФГОС Задание 435

 

\[\boxed{\text{435.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

\[\mathbf{a}^{\mathbf{0}}\mathbf{= 1.}\]

Решение.

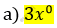
\[если\ x = 2,6:\]

\[3x{^\circ} = 3 \cdot 2,6{^\circ} = 3 \cdot 1 = 3;\]

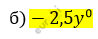
\[если\ y = - 1\frac{2}{3}:\]

\[- 2,5y^{0} = - 2,5 \cdot \left( - 1\frac{2}{3} \right)^{0} =\]

\[= - 2,5 \cdot 1 = - 2,5;\]

\[если\ \ a = - 3;\ \ b = - 8:\ \]

\[10a^{2}b^{0} =\]

\[= 10 \cdot ( - 3)^{2} \cdot ( - 8){^\circ} =\]

\[= 10 \cdot 9 \cdot 1 = 90;\]

\[если\ \ \ a = \frac{2}{3};\ \ c = - \frac{1}{3}:\]

\[27a^{0}c^{3} = 27 \cdot \left( \frac{2}{3} \right)^{0} \cdot \left( - \frac{1}{3} \right)^{3} =\]

\[= 27 \cdot \left( - \frac{1}{27} \right) = - 1.\]

\[\boxed{\text{435\ (435).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ сторона\ бассейна\ \]

\[равна\ a,\ тогда\ его\ объем\ равен\ \]

\[V_{1} = a^{3}.\]

\[Если\ сторону\ увеличили\ \]

\[в\ 2\ раза,\ то\ объем\ стал\ равен\ \]

\[V_{2} = (2a)^{3} = 8a^{3},\]

\[то\ есть\ увеличился\ в\ 8\ раз.\]

\[Значит,\ и\ время,\ затраченное\ на\ \]

\[наполнение\ бассейна,\ должно\]

\[увеличиться\ в\ 8\ раз:\ \ \]

\[8 \cdot 40 = 320\ минут\ или\ \]

\[\ 5\ часов\ 20\ минут \Longrightarrow а\ это\ \]

\[больше\ 5\ часов.\]

\[Ответ:не\ успеют.\]