Решебник по алгебре 7 класс Макарычев ФГОС Задание 1186

 

\[\boxed{\text{1186.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

\[\textbf{а)}\ \left\{ \begin{matrix} \frac{x}{5} = 1 - \frac{7}{15}\ \ | \cdot 15 \\ 2x - 5y = 0\ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 3x = 15 - y\ \ | \cdot 5 \\ 2x = 5y\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 15x = 75 - 5y \\ 2x = 5y\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

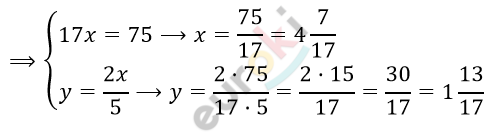
\[Ответ:\left( 4\frac{7}{17};1\frac{13}{17} \right).\]

\[\textbf{б)}\ \left\{ \begin{matrix} 3m + 5n = 1\ \ \ \ \ \ \ \ \\ \frac{m}{4} + \frac{3n}{5} = 1\ \ | \cdot 20 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 3m + 5n = 1\ \ | \cdot ( - 5) \\ 5m + 12n = 20\ \ \ | \cdot 3 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} - 15m - 25n = - 5 \\ 15m + 36n = 60\ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[Ответ:(5;\ - 8).\]

\[\textbf{в)}\ \left\{ \begin{matrix} 4x - 3y = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{2x + 1}{6} = \frac{9 - 5y}{8}\ \ | \cdot 24 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 4x - 3y = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 4 \cdot (2x + 1) = 3 \cdot (9 - 5y) \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 4x - 3y = 1\ \ \ \ \ \ | \cdot 5 \\ 8x + 4 = 27 - 15y \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 20x - 15y = 5 \\ 8x + 15y = 23 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 28x = 28 \longrightarrow x = 1 \\ 3y = 4x - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[3y = 4 \cdot 1 - 1 = 3 \rightarrow y = 1\]

\[Ответ:(1;1).\]

\[\textbf{г)}\ \left\{ \begin{matrix} 3q = 4p - 7\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{1 - 3q}{4} = \frac{4 - 2p}{3}\ \ | \cdot 12 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 3q = 4p - 7\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 3 \cdot (1 - 3q) = 4 \cdot (4 - 2p) \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 3q - 4p = - 7\ \ | \cdot 2 \\ 3 - q = 16 - 8p\ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} 6q - 8p = - 14 \\ 8p - 9q = 13\ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} - 3q = - 1 \longrightarrow q = \frac{1}{3} \\ 4p = 3q + 7\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[4p = 3 \cdot \frac{1}{3} + 7 = 8 \longrightarrow p = 2\]

\[Ответ:\left( \frac{1}{3};2 \right).\]

\[\boxed{\text{1186\ (1186).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Кратное число – это число, которое делится на другое число без остатка.

Запись чисел вида \(\overline{\mathbf{\text{xyz}}}\) означает, что каждая буква – это цифра, а вместе они образуют десятичное число, которое можно представить в виде суммы разрядных слагаемых:

\[\overline{\mathbf{\text{xyz}}}\mathbf{= 100}\mathbf{x + 10}\mathbf{y + z.}\]

При решении уравнения используем следующее:

1. Чтобы вынести общий множитель за скобки, надо каждый член многочлена разделить на их наибольший общий делитель и результат записать в скобках, а общий множитель за скобками:

\[\mathbf{ab + b}\mathbf{m}\mathbf{= b \bullet}\left( \mathbf{a + m} \right)\mathbf{.}\]

2. Способ группировки:

1) сгруппировать члены выражения так, чтобы слагаемые в каждой группе имели общий множитель;

2) в каждой группе вынести общий множитель за скобки;

3) образовавшийся общий для обеих групп множитель вынести за скобки.

\[\mathbf{ax + bx + 5}\mathbf{a + 5}\mathbf{b =}\left( \mathbf{ax + bx} \right)\mathbf{+}\left( \mathbf{5}\mathbf{a + 5}\mathbf{b} \right)\mathbf{=}\mathbf{x \bullet}\left( \mathbf{a + b} \right)\mathbf{+ 5 \bullet}\left( \mathbf{a + b} \right)\mathbf{=}\]

\[\mathbf{=}\left( \mathbf{a + b} \right)\left( \mathbf{x + 5} \right)\mathbf{.}\]

3. Если один из множителей делится на некоторое число, то и произведение делится на это же число.

Решение.

\[Пусть\ a - первая\ и\ четвертая\ \]

\[цифры,\ b - вторая\ и\ \]

\[пятая\ цифры,c - третья\ и\ \]

\[шестая\ цифры:\ \]

\[= 1001 \cdot (100a + 10b + c) =\]

\[= 1001\overline{\text{abc}} = 7 \cdot 11 \cdot 13\overline{\text{abc}},\]

\[значит,\ это\ число\ кратно\ \ 7,\ \]

\[11\ и\ 13.\]