Решебник по алгебре 7 класс Макарычев ФГОС Задание 1139

 

\[\boxed{\text{1139.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

\[Пусть\ x - искомое\ число.\ Если\ \ \]

\[(100 - x)\ разделили\ на\ 5,\ то\ \]

\[остаток\ \]

\[равен\ 1;если\ \ (100 - x)\ \]

\[разделили\ на\ 7,\ то\ остаток\ \]

\[равен\ 1.\ При\ этом\]

\[первое\ частное\ больше\ \]

\[второго\ на\ 2.\]

\[Составим\ и\ решим\ систему\]

\[\ уравнений:\]

\[\left\{ \begin{matrix} 100 - x = 5 \cdot (y + 2) + 1 \\ 100 - x = 7y + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 100 - x = 5y + 10 + 1 \\ 7y + x = 99\ \ \ \ \ \ \ | \cdot ( - 1) \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 5y + x = 89\ \ \ \ \ \ \ \\ - 7y - x = - 99 \\ \end{matrix} \right.\ \Longrightarrow\]

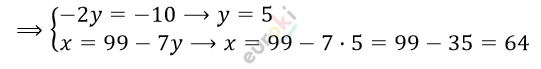
\[Ответ:64 - искомое\ число.\]

\[\boxed{\text{1139\ (1139).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Целые числа – это все положительные, отрицательные числа и ноль, которые не содержат дробной части (примеры целых чисел: 3, -3).

Координаты точки – это пара чисел, в которой на первом месте стоит абсцисса (x), а на втором – ордината точки (у): A (x; y).

Чтобы выяснить является ли решением уравнения пара значений переменных x и y, нужно в уравнение вместо x и y подставить данные координаты точки. Если получилось верное равенство, то точка является решением уравнения.

Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

Решение.

\[ax + by = 81;\ \ \ (15;40):\ \ \]

\[15a + 40b = 81\ \ \ |:5\]

\[3a + 8b = 16,2 \Longrightarrow\]

\[\text{a\ }и\ b - не\ целые\ числа,\ \]

\[а\ это\ противоречит\ условию\ \]

\[задачи \Longrightarrow\]

\[пара\ чисел\ (15;40) - не\ может\ \]

\[быть\ решением\ этого\ \]

\[уравнения.\]