Решебник по алгебре 7 класс Макарычев ФГОС Задание 111

 

\[\boxed{\text{111.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Распределительное свойство:

\[a \cdot (b + c) = ab + ac.\]

Решение.

Тождество – это равенство,

верное при любых значениях

переменных.

\[\textbf{а)}\ 7 \cdot (x - y) = 7x - 7y\]

\[\textbf{б)}\ (a - 4b) \cdot 3 = a \cdot 3 - 4b \cdot 3 =\]

\[= 3a - 12b\]

\[\textbf{в)} - 23 \cdot (2a - 3b + 1) =\]

\[= - 23 \cdot 2a - 3b \cdot ( - 23) - 23 \cdot 1 =\]

\[= - 46a + 69b - 23\]

\[\textbf{г)}\ 1,5 \cdot ( - 3x + 4y - 5z) =\]

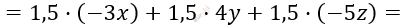
\[= - 4,5x + 6y - 7,5z\ \]

\[\boxed{\text{111\ (111).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ 5 \cdot (2x - 1) = 8x + 1\]

\[10x - 5 = 8x + 1\]

\[Подставим\ x = 3:\]

\[10 \cdot 3 - 5 = 8 \cdot 3 + 1\]

\[30 - 5 = 24 + 1\]

\[25 = 25\]

\[\Longrightarrow x = 3 - является\ корнем\ \]

\[уравнения.\]

\[\textbf{б)}\ (x - 4)(x + 4) = 7\]

\[Подставим\ \ x = 3:\]

\[(3 - 4)(3 + 4) = 7\]

\[- 1 \cdot 7 = 7\]

\[- 7 \neq 7\]

\[\Longrightarrow x = 3 - не\ является\ корнем\ \]

\[уравнения.\]