Алгебра
Английский
Биология
География
Геометрия
Русский
История
Обществознание
Физика
Химия
Информатика
Литература
МатематикаГДЗ по алгебре 7 класс Макарычев ФГОС Задание 1076
Задание 1076
\[\boxed{\text{1076.}\text{\ }еуроки - ответы\ на\ пятёрку}\]
\[\textbf{а)}\ \left\{ \begin{matrix} x - y = 1\ \\ x + 3y = 9 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x = 1 + y\ \ \\ x = 9 - 3y \\ \end{matrix} \right.\ \]
| \[x\] | \[1\] | \[2\] |
|---|---|---|
| \[y\] | \[0\] | \[1\] |
| \[x\] | \[0\] | \[6\] |
|---|---|---|
| \[y\] | \[3\] | \[1\] |
\[Решение:(3;2).\]
\[\textbf{б)}\ \left\{ \begin{matrix} x + 2y = 4\ \ \ \ \ \ \ \\ - 2x + 5y = 10 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} x = 4 - 2y\ \ \ \\ x = 2,5y - 5 \\ \end{matrix} \right.\ \]
| \[x\] | \[4\] | \[0\] |
|---|---|---|
| \[y\] | \[0\] | \[2\] |
| \[x\] | \[- 5\] | \[0\] |
|---|---|---|
| \[y\] | \[0\] | \[2\] |
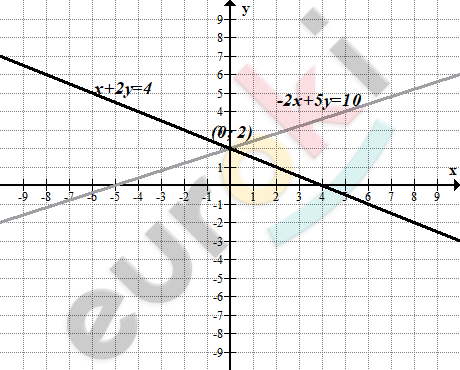
\[Решение:(0;2).\]
\[\textbf{в)}\ \left\{ \begin{matrix} x + y = 0\ \ \ \ \ \ \ \ \ \ \\ - 3x + 4y = 14 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\ \left\{ \begin{matrix} x = - y\ \ \ \ \ \ \ \ \ \ \ \\ x = \frac{4}{3}y - \frac{14}{3} \\ \end{matrix} \right.\ \]
| \[x\] | \[0\] | \[1\] |
|---|---|---|
| \[y\] | \[0\] | \[- 1\] |
| \[x\] | \[- \frac{10}{3}\] | \[- 2\] |
|---|---|---|
| \[y\] | \[1\] | \[2\] |
\[Решение:( - 2;2).\]
\[\textbf{г)}\ \left\{ \begin{matrix} 3x - 2y = 6\ \ \ \ \ \ \ \ \ \ \\ 3x + 10y = - 12 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]
\[\text{\ \ }\left\{ \begin{matrix} y = 1,5x - 3\ \ \ \ \ \ \ \ \ (1) \\ y = - 1,2 - 0,3x\ \ (2) \\ \end{matrix} \right.\ \]
| \[x\] | \[0\] | \[2\] |
|---|---|---|
| \[y\] | \[- 3\] | \[0\] |
| \[x\] | \[- 4\] | \[0\] |
|---|---|---|
| \[y\] | \[0\] | \[- 1,2\] |
\[Решение:\ (1; - 1,5).\]
