Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 7 класс Макарычев ФГОС Контрольные вопросы и задания к параграфу 8
Контрольные вопросы и задания к параграфу 8
1
\[\boxed{\text{1.}\text{\ }}\]
\[Многочленом\ называется\ \]
\[сумма\ одночленов.\]
2
\[\boxed{\text{2.}\text{\ }}\]
\[Чтобы\ привести\ многочлен\ к\]
\[\ стандартному\ виду,\ надо:\]
\[1)\ каждый\ его\ член\ \]
\[представить\ в\ стандартном\ \]
\[виде;\]
\[2)\ привести\ подобные\ члены.\]
\[5a^{2}x + ax^{2} - 4ax \cdot \frac{1}{2}x = 5a^{2}x +\]
\[+ ax^{2} - 2ax^{2} =\]
\[= \left( ax^{2} - 2ax^{2} \right) + 5a^{2}x =\]
\[= - ax^{2} + 5a^{2}\text{x.}\]
3
\[\boxed{\text{3.}\text{\ }}\]
\[Степенью\ многочлена\ \]
\[стандартного\ вида\ \]
\[называется\ наибольшая\]
\[из\ степеней\ входящих\ в\ него\ \]
\[одночленов.\]
\[Степенью\ произвольного\ \]
\[многочлена\ называют\ \]
\[степень\ тождественного\]
\[ему\ многочлена\ стандартного\ \]
\[вида.\]
\[15xy^{2} + 7xy + 8 \Longrightarrow многочлен\ \]
\[третьей\ степени.\]
4
\[\boxed{\text{4.}\text{\ }}\]
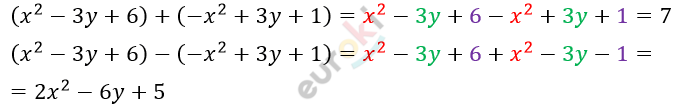
5
\[\boxed{\text{5.}\text{\ }}\]
\[\textbf{а)}\ 5x^{2} + ( - x + 4)\]
\[\textbf{б)}\ 5x^{2} - (x - 4)\]
\[\boxed{\text{Контрольные}\text{\ }\text{вопросы}\text{\ }\text{и}\text{\ }\text{задания}\text{\ }\text{к}\text{\ }\text{параграфу}\text{\ }\text{8.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\boxed{\text{1.}\text{\ }}\]
\[Примеры\ одночленов\ \]
\[стандартного\ вида:\]
\[12ab^{3};\ \ \ \ \ \ \ \ \ 2xyz;\ \ \ \ 0,5cb^{5}.\]
\[\boxed{\text{2.}\text{\ }}\]
\[5ab^{2} \cdot \left( - 3a^{4}b \right) = - 15a^{5}b^{3}\]
\[коэффициент\ равен\ ( - 15).\]
\[\boxed{\text{3.}\text{\ }}\]
\[Степенью\ одночлена\ называют\ \]
\[сумму\ показателей\ степеней\ \]
\[всех\ входящих\ в\ него\ \]
\[переменных.\]
\[Если\ одночлен\ не\ содержит\ \]
\[переменных\ \]
\[(то\ есть\ является\ числом),\ то\]
\[его\ степень\ считают\ равной\ \]
\[нулю.\]
\[Одночлен\ пятой\ степени:\]
\[5a^{2}b^{3}.\]
\[\boxed{\text{4.}\text{\ }}\]
\[Свойства\ функции\ y = x^{2}:\]
\(если\ x = 0;\)
\[то\ y = 0 \Longrightarrow график\ функции\ \]
\[проходит\ через\ начало\ \]
\(координат;\)
\(если\ x \neq 0;\)
\(то\ y > 0 \Longrightarrow все\ точки\ \)
\(графика,\ кроме\ точки\ (0;0),\ \)
\(расположены\ выше\ оси\ x;\)
\(противоположным\ \)
\[значениям\ x\ соответствует\ \]
\(одно\ и\ то\ же\) \(значение\ y,\)
\[значит,\ точки\ графика,\ \]
\[имеющие\ \]
\[противоположные\ \ \]
\(абсциссы,симметричны\ \)
\(относительно\ оси\ y.\)
\[\boxed{\text{5.}\text{\ }}\]
\[Свойства\ функции\ y = x^{3}:\]
\(если\ x = 0;\)
\[то\ y = 0 \Longrightarrow график\ функции\ \]
\[проходит\ через\ начало\]
\(координат;\)
\(если\ x > 0;то\ y > 0;\ \ \ \)
\(если\ x < 0;\ \ то\ y < 0 \Longrightarrow\)
\[\Longrightarrow график\ функции\]
\[расположен\ в\ первой\ и\ \]
\[третьей\ координатных\ \]
\[четвертях;\]
\(противоположным\ \)
\[значениям\ \text{x\ }соответствуют\ \]
\[противоположные\]
\(значения\ y;\ \ \ значит,\ точки\ \)
\(графика,\ имеющие\ \)
\(противоположные\ абсциссы,\ \)
\(расположены\ симметрично\ \)
\(относительно\ начала\ \)
\(координат.\)
