Решебник по алгебре 7 класс Макарычев ФГОС Контрольные вопросы и задания к параграфу 12

 

1

\[\boxed{\text{1.}\text{\ }}\]

\[Произведение\ разности\ двух\]

\[\ выражений\ и\ их\ суммы\ равно\]

\[\ разности\]

\[квадратов\ этих\ выражений:\]

\[(a - b)(a + b) = a^{2} - b^{2}.\]

\[Доказательство:\]

2

\[\boxed{\text{2.}\text{\ }}\]

\[Разность\ квадратов\ двух\ \]

\[выражений\ равна\ \]

\[произведению\ разности\]

\[этих\ выражений\ и\ их\ суммы:\]

\[a^{2} - b^{2} = (a - b)(a + b).\]

3

\[\boxed{\text{3.}\text{\ }}\]

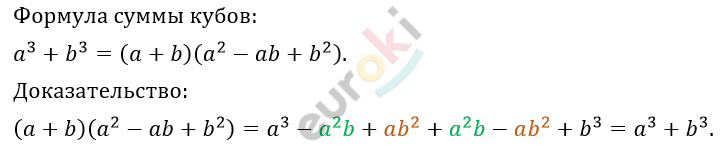
4

\[\boxed{\text{4.}\text{\ }}\]

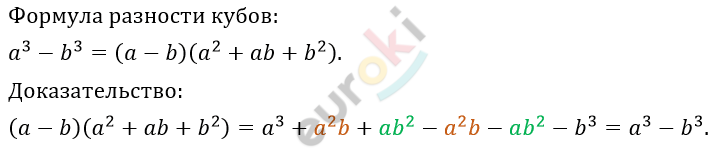
5

\[\boxed{\text{5.}\text{\ }}\]

\[16t^{2} - 1 = (4t - 1)(4t + 1)\]

\[p^{3} + 8 = (p + 2)\left( p^{2} - 2p + 4 \right)\]

\[m^{3} - 27 =\]

\[= (m - 3)(m^{2} + 3m + 9)\]

\[\boxed{\text{Контрольные}\text{\ }\text{вопросы}\text{\ }\text{и}\text{\ }\text{задания}\text{\ }\text{к}\text{\ }\text{параграфу}\text{\ }\text{12.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\boxed{\text{1.}\text{\ }}\]

\[Формула\ квадрата\ суммы:\]

\[(a + b)^{2} = a^{2} + 2ab + b^{2}.\]

\[Доказательство:\]

\[(a + b)^{2} = (a + b)(a + b) =\]

\[= a^{2} + 2ab + b^{2}.\]

\[\boxed{\text{2.}\text{\ }}\]

\[Формула\ квадрата\ разности:\]

\[(a - b)^{2} = a^{2} - 2ab + b^{2}.\]

\[Доказательство:\]

\[(a - b)^{2} = (a - b)(a - b) =\]

\[= a^{2} - 2ab + b^{2}.\]

\[\boxed{\text{3.}\text{\ }}\]

\[25y^{2} + 40y + 16 = (5y + 4)^{2}\]

\[\boxed{\text{4.}\text{\ }}\]

\[81x^{2} - 18x + 1 = (9x - 1)^{2}\]

\[\boxed{\text{5.}\text{\ }}\]

\[Формула\ куба\ суммы:\]

\[(a + b)^{3} =\]

\[= a^{3} + 3a^{2}b + 3ab^{2} + b^{3}.\]

\[Пример:\ \]

\[(a + 2b)^{3} =\]

\[= a^{3} + 6a^{2}b + 12ab^{2} + 8b^{3}.\]

\[\boxed{\text{6.}\text{\ }}\]

\[Формула\ куба\ разности:\]

\[(a - b)^{3} =\]

\[= a^{3} - 3a^{2}b + 3ab^{2} - b^{3}.\]

\[(3x - y)^{3} =\]

\[= 27x^{3} - 27x^{2}y + 9xy^{2} - y^{3}.\]