Решебник по алгебре 7 класс Мерзляк контрольные работы КР-8. Обобщение и систематизация знаний учащихся Вариант 1

Условие:

1. Упростите выражение (5a-4)^2-(2a-1)(3a+7).

2. Разложите на множители:

1) 5x^2 y^2-45y^2 c^2

2) 2x^2+24xy+72y^2

3. График функции y = kx + b пересекает оси координат в точках A (0; –6) и B (3; 0). Найдите значения k и b.

4. Решите систему уравнений

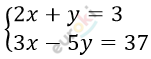
5. Найдите четыре последовательных натуральных числа таких, что произведение третьего и четвёртого из этих чисел на 22 больше произведения первого и второго.

6. Решите уравнение x^2+y^2-2x+6y+10=0.

Решение:

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[(5a - 4)^{2} - (2a - 1)(3a + 7) =\]

\[= 25a^{2} - 40a + 16 -\]

\[- \left( 6a^{2} - 3a + 14a - 7 \right) =\]

\[= 25a^{2} - 40a + 16 - 6a^{2} - 11a + 7 =\]

\[= 19a^{2} - 51a + 23.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[1)\ 5x^{2}y^{2} - 45y^{2}c^{2} =\]

\[= 5y^{2}\left( x^{2} - 9c^{2} \right) =\]

\[= 5y^{2}(x - 3c)(x + 3c)\]

\[2)\ 2x^{2} + 24xy + 72y^{2} =\]

\[= 2 \cdot \left( x^{2} + 12xy + 36y^{2} \right) =\]

\[= 2 \cdot (x + 6y)(x + 6y)\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[y = kx + b;\ \ A(0; - 6);\ \ B(3;0).\]

\[A(0;\ - 6):\]

\[- 6 = 0k + b\]

\[b = - 6.\]

\[B(3;0);\ \ b = - 6:\]

\[0 = 3k - 6\]

\[3k = 6\]

\[k = 2.\]

\[Ответ:k = 2;\ \ b = - 6.\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[\left\{ \begin{matrix} 2x + y = 3\ \ \ \ | \cdot 5\ \\ 3x - 5y = 37\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]

\[\left\{ \begin{matrix} 10x + 5y = 15 \\ 3x - 5y = 37\ \ \\ \end{matrix} \right.\ ( + )\]

\[13x = 52\]

\[x = 4.\]

\[y = 3 - 2x = 3 - 2 \cdot 4 =\]

\[= 3 - 8 = - 5.\]

\[\left\{ \begin{matrix} x = 4\ \ \ \\ y = - 5 \\ \end{matrix} \right.\ \]

\[Ответ:(4; - 5).\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[Пусть\ n;n + 1;n + 2;n + 3 - \ \]

\[четыре\ последовательных\ \]

\[натуральных\ числа.\]

\[(n + 2)(n + 3) - произведение\ \]

\[третьегои\ четвертого\ чисел;\]

\[n(n + 1) - произведение\ \ \]

\[первого\ и\ второго\ чисел.\]

\[Составим\ уравнение:\]

\[(n + 2)(n + 3) - n(n + 1) = 22\]

\[n^{2} + 2n + 3n + 6 - n^{2} - n = 22\]

\[4n = 22 - 6\]

\[4n = 16\]

\[n = 4 - первое\ число.\]

\[n + 1 = 4 + 1 = 5 - второе\ \]

\[число.\]

\[n + 2 = 4 + 2 = 6 - третье\ \]

\[число.\]

\[n + 3 = 4 + 3 = 7 - четвертое\ \]

\[число.\]

\[Ответ:числа\ 4,\ 5,\ 6,\ 7.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[x^{2} + y^{2} - 2x + 6y + 10 = 0\]

\[\left( x^{2} - 2x + 1 \right) + \left( y^{2} + 6y + 9 \right) = 0\]

\[(x - 1)^{2} + (y + 3)^{2} = 0\]

\[\left\{ \begin{matrix} x - 1 = 0 \\ y + 3 = 0 \\ \end{matrix} \right.\ \ \]

\[\left\{ \begin{matrix} x = 1\ \ \ \\ y = - 3 \\ \end{matrix} \right.\ \]

\[Ответ:(1;\ - 3).\]