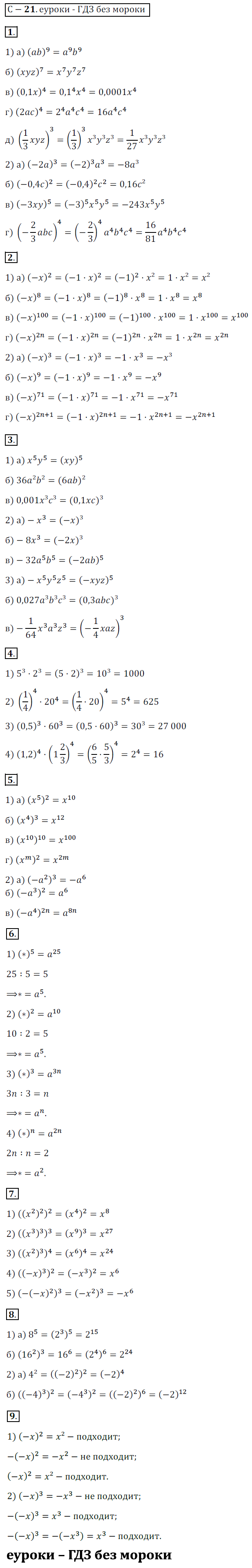Решебник по алгебре 7 класс Звавич дидактические материалы С-21. Возведение в степень произведения и степени | Номер Вариант 1

Условие:

1. Возведите в степень произведение:

1) а) (ab)^9

б) (xyz)^7

в) (0,1x)^4

г) (2ac)^4

д) (1/3*xyz)^3

2) а) (-2a)^3

б) (-0,4c)^2

в) (-3xy)^5

г) (-2/3*abc)^4

2. Выполните возведение в степень, представив предварительно основание степени в виде произведения множителей -1 и x:

1) а) (-x)^2

б) (-x)^8

в) (-x)^100

г) (-x)^2n

2) а) (-x)^3

б) (-x)^9

в) (-x)^71

г) (-x)^(2n+1)

3. Представьте произведение в виде степени:

1) а) x^5y^5

б) 36a^2b^2

в) 0,001x^3c^3

2) а) –x^3

б) -8x^3

в) -32a^5b^5

3) а) –x^5y^5z^5

б) 0,027a^3b^3c^3

в) -1/64*x^3a^3z^3

4. Вычислите значение выражения, используя свойство степени произведения:

1) 5^3*2^3

2) (1/4)^4*20^4

3) (0,5)^3*60^3

4) (1,2)^4*(1 2/3)^4

5. Выполните возведение в степень:

1) а) (x^5)^2

б) (x^4)^3

в) (x^10)^10

г) (x^m)^2

2) а) (-a^2)^3

б) (-a^3)^2

в) (-a^4)^2n

6. Замените значок «*» таким выражением, чтобы выполнялось равенство:

1) (*)^5=a^25

2) (*)^2=a^10

3) (*)^3=a^3n

4) (*)^n=a^2n

7. Упростите выражение:

1) ((x^2)^2)^2

2) ((x^3)^3)^3

3) ((x^2)^3)^4

4) ((-x)^3)^2

5) (-(-x)^2)^3

8. Представьте выражение в виде степени:

1) с основанием 2:

а) 8^5

б) (16^2)^3

2) с основанием (-2):

а) 4^2

б) ((-4)^3)^2

9. Среди выражений укажите такие, которые:

1) тождественно равны x^2:

(-x)^2; -(-x)^2; -(-x^2);

2) тождественно равны x^3:

(-x)^3; -(-x^3); -(-x)^3.