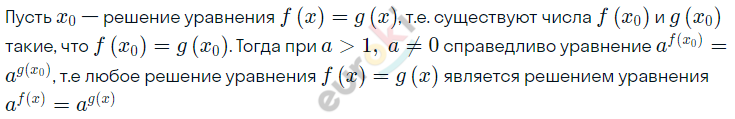Решебник по алгебре 11 класс Никольский Параграф 7. Равносильность уравнений и неравенств Задание 2

\[\boxed{\mathbf{2.}}\]

\[\textbf{а)}\ Докажем,\ что\ для\ любого\ \]

\[нечетного\ числа\ 2m + 1;m \in N\]

\[любое\ решение\ уравнения\]

\[\text{\ f}(x) = g(x)\ является\ \]

\[решением\]

\[уравнения\ \sqrt[{2m + 1}]{f(x)} =\]

\[= \sqrt[{2m + 1}]{g(x)}.\]

\[Докажем\ обратное.\]

\[\textbf{б)}\ Докажем,\ что\ если\ a > 1;\]

\[a \neq 0,\ то\ любое\ решение\]

\[\ уравнения\]

\[a^{f(x)} = a^{g(x)}\ является\]

\[{\ решением\ уравнения }{\ f(x) = g(x).}\]

\[Докажем\ обратное.\ \]