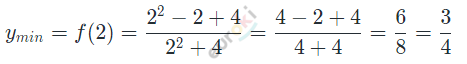Решебник по алгебре 11 класс Никольский Параграф 5. Применение производной Задание 84

\[\boxed{\mathbf{84}\mathbf{.}}\]

\[f(x) = \frac{x^{2} - x + 4}{x + 4};\ \ x \in \lbrack 0; + \infty)\]

\[D(f) = R;\]

\[f(x) - определена\ во\ всех\]

\[\ точках\ полуинтервала.\]

\[f^{'}(x) = 0:\]

\[\frac{x^{2} - 4}{\left( x^{2} + 4 \right)^{2}} = 0\]

\[x^{2} - 4 = 0\]

\[(x - 2)(x + 2) = 0\]

\[x_{1} = 2 \in \lbrack 0; + \infty);\]

\[x_{2} = - 2\ (не\ принадлежит).\]

\[x = 2 \rightarrow единственная\ \]

\[критическая\ точка\ функции\ \]

\[на\ промежутке.\]

\[f^{''}(x) = \frac{1}{16} > 0;\]

\[x = 2 \rightarrow точка\ минимума.\]