Решебник по алгебре 11 класс Никольский Параграф 4. Производная Задание 44

\[\boxed{\mathbf{44}\mathbf{.}}\]

\[\textbf{а)}\ f(x) = \frac{4^{x}}{2^{x}} = \left( \frac{4}{2} \right)^{x} = 2^{x};\ \]

\[\ x \in R\]

\[f^{'}(x) = 2^{x}\ln 2;\ \ x \in R.\]

\[{б)\ f(x) = \frac{3^{x}}{9^{x}} = \left( \frac{3}{9} \right)^{x} = \left( \frac{1}{3} \right)^{x}; }{\ \ x \in R}\]

\[f^{'}(x) = \left( \frac{1}{3} \right)^{x}\ln\frac{1}{3} = \frac{1^{x}}{3^{x}}\ln 3^{- 1} =\]

\[= \ln\frac{3^{- 1}}{3^{x}} = - \frac{\ln 3}{3^{x}};\ \ x \in R.\]

\[\textbf{в)}\ f(x) = \frac{2^{x} + 4^{x}}{2^{x}} = \frac{2^{x}}{2^{x}} + \frac{4^{x}}{2^{x}} =\]

\[= 1 + \left( \frac{4}{2} \right)^{x} = 1 + 2^{x};\ \ x \in R\]

\[f^{'}(x) = 0 + 2^{x}\ln 2 = 2^{x}\ln 2;\ \]

\[\ x \in R.\]

\[\textbf{г)}\ f(x) = \frac{3^{x}}{3^{x} + 9^{x}} =\]

\[= \frac{3^{x}}{3^{x} + \left( 3^{x} \cdot 3^{x} \right)} = \frac{3^{x}}{3^{x}\left( 1 + 3^{x} \right)} =\]

\[= \frac{1}{1 + 3^{x}};\ \ x \in R\]

\[f^{'}(x) = \left( \frac{1}{1 + 3^{x}} \right)^{'} =\]

\[= \frac{1^{'} \cdot (1 + 3)^{x} - 1 \cdot \left( 1 + 3^{x} \right)^{'}}{\left( 1 + 3^{x} \right)^{2}} =\]

\[= \frac{0 \cdot \left( 1 + 3^{x} \right) - \left( 0 + 3^{x}\ln 3 \right)}{\left( 1 + 3^{x} \right)^{2}} =\]

\[= - \frac{3^{x}\ln 3}{\left( 1 + 3^{x} \right)^{2}};\ \ x \in R.\]

\[\textbf{д)}\ f(x) = \frac{2^{x} - 4^{x}}{2^{x} + 4^{x}} =\]

\[= \frac{2^{x}(1 - 2^{x})}{2^{x}\left( 1 + 2^{x} \right)} = \frac{1 - 2^{x}}{1 + 2^{x}}\]

\[f^{'}(x) = \left( \frac{1 - 2^{x}}{1 + 2^{x}} \right)^{'} =\]

\[= \frac{- 2 \cdot 2^{x}\ln 2}{\left( 1 + 2^{x} \right)^{2}} = - \frac{2^{x + 1}\ln 2}{\left( 1 + 2^{x} \right)^{2}};\ \ \]

\[x \in R.\]

\[\textbf{е)}\ f(x) = \frac{3^{x} - 9^{x}}{3^{x} + 9^{x}}\]

\[f^{'}(x) = \left( \frac{1 - 3^{x}}{1 + 3^{x}} \right) =\]

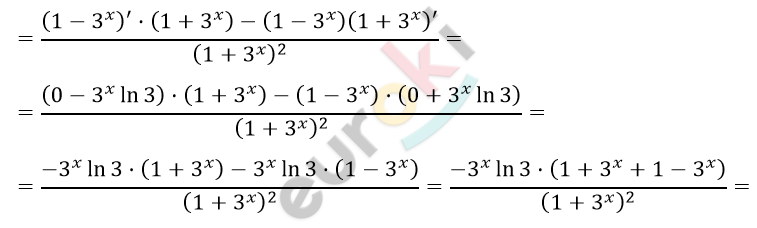
\[= \frac{- 2 \cdot 3^{x}\ln 3}{\left( 1 + 3^{x} \right)^{2}};\ \ \ x \in R.\]

\[\textbf{ж)}\ f(x) = \frac{\lg x}{\lg e} = \ln x;\]

\[f^{'(x)} = \left( \ln x \right)^{'} = \frac{1}{x};\ \ \ x > 0.\]

\[\textbf{з)}\ f(x) = \frac{\ln x}{\ln 10} = \log_{10}x = \lg x;\]

\[f^{'}(x) = \left( \lg x \right)^{'} = \frac{1}{x\ln 10};\ \ x > 0.\]

\[\textbf{и)}\ f(x) = \frac{\lg x}{\lg 2} = \log_{2}x;\]

\[f^{'}(x) = \left( \log_{2}x \right)^{'} = \frac{1}{x\ln 2};\ \ x > 0.\ \]