Решебник по алгебре 11 класс Никольский Параграф 3. Обратные функции Задание 15

\[\boxed{\mathbf{15}\mathbf{.}}\]

\[\textbf{а)}\ y = \arcsin x\ \]

\[Функция\ ограничена.\]

\[Принимает\ наименьшее\ \]

\[значение\ y = - \frac{\pi}{2}\ при\ x = - 1;\]

\[наибольшее\ значение\ \]

\[y = \frac{\pi}{2}\ при\ x = 1.\]

\[Функция\ нечетная.\]

\[(0;0) - единственная\ точка\ \]

\[пересечения\ с\ осями.\]

\[Возрастает\ на\ отрезке\ \]

\[\lbrack - 1;1\rbrack - на\ всей\ области\]

\[\ определения.\]

\[Непрерывна\ на\ отрезке\ \lbrack - 1;1\rbrack.\]

\[\textbf{б)}\ y = \arccos x\]

\[Функция\ ограничена.\]

\[Принимает\ наименьшее\ \]

\[значение\ y = \pi\ при\ x = - 1;\]

\[наибольшее\ значение\ y = 0\]

\[\ при\ x = 1.\]

\[Функция\ ни\ четная,\ ни\ \]

\[нечетная.\]

\[\left( 0;\frac{\pi}{2} \right);(1;0) - \ точки\ \]

\[пересечения\ с\ осями.\]

\[Убывает\ на\ отрезке\ \lbrack - 1;1\rbrack - на\ \]

\[всей\ области\ определения.\]

\[Непрерывна\ на\ отрезке\ \lbrack - 1;1\rbrack.\]

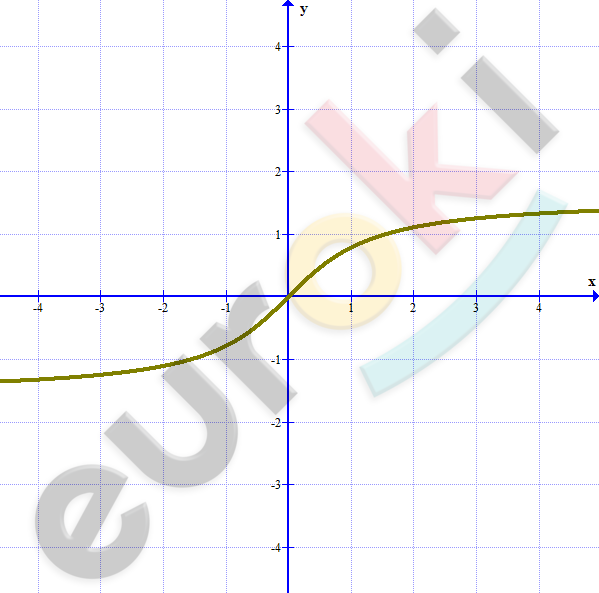
\[\textbf{в)}\ y = arctg\ x\]

\[Функция\ ограничена.\]

\[Не\ имеет\ наибольшего\ и\ \]

\[наименьшего\ значения.\]

\[Функция\ нечетная.\]

\[(0;0) - единственная\ точка\]

\[\ пересечения\ с\ осями.\]

\[Возрастает\ на\ R.\]

\[Непрерывна\ на\ R.\]

\[\textbf{г)}\ y = arcctg\ x;\]

\[Функция\ ограничена.\]

\[Не\ имеет\ наибольшего\ и\]

\[\ наименьшего\ значения.\]

\[Функция\ ни\ четная,\ ни\ \]

\[нечетная.\]

\[\left( 0;\frac{\pi}{2} \right) - единственная\ точка\ \]

\[пересечения\ с\ осями.\]

\[Убывает\ на\ R.\]

\[Непрерывна\ на\ R.\]