Решебник по алгебре 11 класс Никольский Параграф 13. Использование свойств функции при решении уравнений и неравенств Задание 25

\[\boxed{\mathbf{25.}}\]

\[\left( \sqrt[4]{\sin x + 2} - \sqrt[4]{\cos x + 2} \right)^{2} \leq 0\]

\[\sqrt[4]{\sin x + 2} - \sqrt[4]{\cos x + 2} = 0\]

\[\sqrt[4]{\sin x + 2} = \sqrt[4]{\cos x + 2}\]

\[\sin x + 2 = \cos x + 2\]

\[\sin x = \cos x\]

\[tgx = 1\]

\[x = \frac{\pi}{4} + \pi k.\]

\[Ответ:x = \frac{\pi}{4} + \pi k.\]

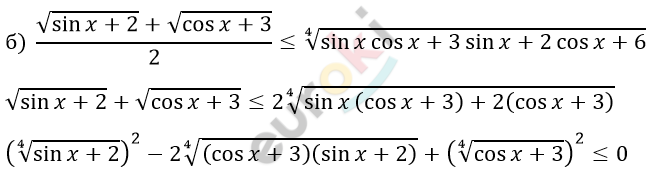
\[\left( \sqrt[4]{\sin x + 2} - \sqrt[4]{\cos x + 3} \right)^{2} \leq 0\]

\[\sqrt[4]{\sin x + 2} - \sqrt[4]{\cos x + 3} = 0\]

\[\sqrt[4]{\sin x + 2} = \sqrt[4]{\cos x + 3}\]

\[\sin x + 2 = \cos x + 3\]

\[\sin x - \cos x = 1\]

\[1)\ \left\{ \begin{matrix} \sin x = 1 \\ \cos x = 0 \\ \end{matrix} \right.\ \]

\[x = \frac{\pi}{2} + 2\pi n.\]

\[2)\ \left\{ \begin{matrix} \sin x = 0\ \ \ \ \\ \cos x = - 1 \\ \end{matrix} \right.\ \]

\[x = \pi + 2\pi n.\]

\[Ответ:x = \frac{\pi}{2} + 2\pi n;\]

\[x = \pi + 2\pi n.\]