Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 11 класс Никольский Параграф 13. Использование свойств функции при решении уравнений и неравенств Задание 1
Задание 1
\[\boxed{\mathbf{1.}}\]
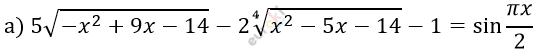
\[\left\{ \begin{matrix} - x^{2} + 9x - 14 \geq 0 \\ x^{2} - 5x - 14 \geq 0\ \ \ \\ \end{matrix} \right.\ \]
\[x^{2} - 9x + 14 \leq 0\]
\[x_{1} + x_{2} = 9;\ \ x_{1} \cdot x_{2} = 14\]
\[x_{1} = 2;\ \ x_{2} = 7;\]
\[(x - 2)(x - 7) \leq 0\]
\[2 \leq x \leq 7.\]
\[x^{2} - 5x - 14 \geq 0\]
\[x_{1} + x_{2} = 5;\ \ \ x_{1} \cdot x_{2} = - 14\]
\[x_{1} = - 2;\ \ \ x_{2} = 7;\]
\[(x + 2)(x - 7) \geq 0\]
\[x \leq - 2;\ \ \ x \geq 7.\]
\[Решение\ системы:\ \ x = 7.\]
\[Проверка:\]
\[5 \cdot 0 - 2 \cdot 0 - 1 = \sin\frac{7\pi}{2}\]
\[- 1 = - 1.\]
\[Ответ:x = 7.\]
\[\left\{ \begin{matrix} - x^{2} + 11x - 30 \geq 0 \\ x^{2} - 7x + 6 \geq 0\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[x^{2} - 11x + 30 \leq 0\]
\[x_{1} + x_{2} = 11;\ \ x_{1} \cdot x_{2} = 30\]
\[x_{1} = 5;\ \ \ x_{2} = 6;\]
\[(x - 5)(x - 6) \leq 0\]
\[5 \leq x \leq 6.\]
\[x^{2} - 7x + 6 \geq 0\]
\[x_{1} + x_{2} = 7;\ \ \ x_{1} \cdot x_{2} = 6\]
\[x_{1} = 1;\ \ \ x_{2} = 6;\]
\[(x - 1)(x - 6) \geq 0\]
\[x \leq 1;\ \ \ x \geq 6.\]
\[Решение\ системы:\]
\[x = 6.\]
\[Проверка:\]
\[3 \cdot 0 - 4 \cdot 0 = \sin{6\pi}\]
\[0 = 0.\]
\[Ответ:x = 6.\]
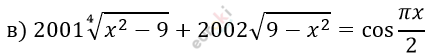
\[\left\{ \begin{matrix} x^{2} - 9 \geq 0 \\ 9 - x^{2} \geq 0 \\ \end{matrix} \right.\ \]
\[x^{2} - 9 \geq 0\]
\[(x + 3)(x - 3) \geq 0\]
\[x \leq - 3;\ \ \ x \geq 3.\]
\[9 - x^{2} \geq 0\]
\[x^{2} - 9 \leq 0\]
\[(x + 3)(x - 3) \leq 0\]
\[- 3 \leq x \leq 3.\]
\[Решение\ системы:\]
\[x = - 3;\ \ x = 3.\]
\[Проверка:\]
\[2001 \cdot 0 - 2002 \cdot 0 = \cos\frac{\pm 3\pi}{2}\]
\[0 = 0.\]
\[Ответ:x = \pm 3.\]
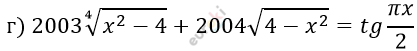
\[\left\{ \begin{matrix} x^{2} - 4 \geq 0 \\ 4 - x^{2} \geq 0 \\ \end{matrix} \right.\ \]
\[x^{2} - 4 \geq 0\]
\[(x + 2)(x - 2) \geq 0\]
\[x \leq - 2;\ \ \ x \geq 2.\]
\[4 - x^{2} \geq 0\]
\[x^{2} - 4 \leq 0\]
\[(x + 2)(x - 2) \leq 0\]
\[- 2 \leq x \leq 2.\]
\[Решение\ системы:\]
\[x = \pm 2.\]
\[Проверка:\]
\[2003 \cdot 0 - 2004 \cdot 0 = tg\ ( \pm \pi)\]
\[0 = 0.\]
\[Ответ:x = \pm 2.\]
