Решебник по алгебре 11 класс Никольский Параграф 10. Равносильность уравнений на множествах Задание 31

\[\boxed{\mathbf{31.}}\]

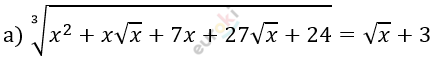
\[M = \lbrack 0; + \infty).\]

\[x^{2} + x\sqrt{x} + 7x + 27\sqrt{x} + 24 =\]

\[= \left( \sqrt{x} + 3 \right)^{2}\]

\[x^{2} + x\sqrt{x} + 7x + 27\sqrt{x} + 24 =\]

\[= x\sqrt{x} + 9x + 27\sqrt{x} + 27\]

\[x^{2} - 2x - 3 = 0\]

\[D_{1} = 1 + 3 = 4\]

\[x_{1} = 1 + 2 = 3;\]

\[x_{2} = 1 - 2 = - 1 < 0.\]

\[Ответ:x = 3.\]

\[\textbf{б)}\ \sqrt[3]{x^{2} + x\sqrt{x} + 27\sqrt{x} - 37} =\]

\[= \sqrt{x} - 3\]

\[M = \lbrack 0; + \infty).\]

\[x^{2} + x\sqrt{x} + 27\sqrt{x} - 37 =\]

\[= \left( \sqrt{x} - 3 \right)^{3}\]

\[x^{2} + x\sqrt{x} + 27\sqrt{x} - 37 =\]

\[= x\sqrt{x} - 9x + 27\sqrt{x} - 27\]

\[x^{2} + 9x - 10 = 0\]

\[x_{1} + x_{2} = - 9;x_{1} \cdot x_{2} = - 10\]

\[x_{1} = - 10 < 0;\ \ \]

\[x_{2} = 1.\]

\[Ответ:x = 1.\]