Решебник по алгебре 11 класс Никольский Параграф 10. Равносильность уравнений на множествах Задание 26

\[\boxed{\mathbf{26}\mathbf{.}}\]

\[\textbf{а)}\ \frac{1}{\sqrt{x - 2}} = (x - 2)^{\cos x}\]

\[x - 2 > 0\]

\[x > 2.\]

\[M = (2; + \infty).\]

\[(x - 2)^{- \frac{1}{2}} = (x - 2)^{\cos x}\]

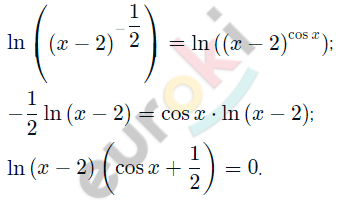
\[\textbf{б)}\ \left( x^{2} + 2 \right)^{\sin x} = \left( x^{2} + 2 \right)^{\cos x}\]

\[x \in R.\]

\[\textbf{в)}\ x^{\log_{\sqrt{x}}{2x}} = 4\]

\[x \in (0;1) \cup (1; + \infty).\]

\[2x = \pm 2\]

\[x = \pm 1.\]

\[Ответ:нет\ корней.\]

\[\textbf{г)}\ x^{2 - lg^{2}x - \lg x^{3}} - \frac{1}{x} = 0\]

\[x \in (0; + \infty).\]