Решебник по алгебре 11 класс Никольский Параграф 10. Равносильность уравнений на множествах Задание 22

\[\boxed{\mathbf{22}\mathbf{.}}\]

\[\textbf{а)}\ 4\cos x\cos{2x} = 1\ \ \ \ \ | \cdot \sin x\]

\[4\cos x\cos{2x}\sin x = \sin x\]

\[\sin{2x}\cos{2x} = \sin x\]

\[\sin{4x} = \sin x\]

\[\sin{4x} - \sin x = 0\]

\[2\sin{\frac{3}{2}x}\cos{\frac{5}{2}x} = 0\]

\[\sin{\frac{3}{2}x} = 0\]

\[\frac{3}{2}x = \pi n\]

\[x_{n} = \frac{2}{3}\text{πn}\]

\[x_{n} = \pm \frac{2\pi}{3} + 2\pi n.\]

\[\cos\frac{5x}{2} = 0\]

\[\frac{5x}{2} = \frac{\pi}{2} + \pi m\]

\[x_{m} = \frac{\pi}{5} + \frac{2}{5}\text{πm}\]

\[x_{m} = \pm \frac{3\pi}{5} + 2\pi m;\]

\[x_{m} = \pm \frac{\pi}{5} + 2\pi m.\]

\[Ответ:\ \pm \frac{2\pi}{3} + 2\pi n;\ \pm \frac{\pi}{5} + 2\pi m;\ \]

\[\pm \frac{3\pi}{5} + 2\pi m.\]

\[\textbf{б)}\ 4\cos x\cos{2x} = - 1\ \ \ \ | \cdot \sin x\]

\[4\cos x\cos{2x}\sin x = - \sin x\]

\[\sin{2x}\cos{2x} = - \sin x\]

\[\sin{4x} = - \sin x\]

\[\sin{4x} + \sin x = 0\]

\[2\sin\left( \frac{5}{2}x \right)\cos\left( \frac{3}{2}x \right) = 0\]

\[\sin\frac{5x}{2} = 0\]

\[\frac{5x}{2} = \pi n\]

\[x = \frac{2}{5}\text{πn}\]

\[x_{n} = \pm \frac{\pi}{5} + 2\pi n;\]

\[x_{n} = \pm \frac{2\pi}{5} + 2\pi n.\]

\[\cos\frac{3x}{2} = 0\]

\[\frac{3x}{2} = \frac{\pi}{2} + \pi m\]

\[x = \frac{\pi}{3} + \frac{2}{3}\text{πm}\]

\[x_{m} = \pm \frac{\pi}{3} + 2\pi m.\]

\[Ответ:\ \pm \frac{\pi}{3} + 2\pi m;\ \pm \frac{\pi}{5} + 2\pi n;\ \]

\[\pm \frac{2\pi}{5} + 2\pi n.\]

\[8\cos x\cos{2x}\cos{4x}\sin x = \sin x\]

\[4\sin{2x}\cos{2x}\cos{4x} = \sin x\]

\[2\sin{4x}\cos{4x} = \sin x\]

\[\sin{8x} - \sin x = 0\]

\[2\sin\left( \frac{7x}{2} \right)\cos\left( \frac{9x}{2} \right) = 0\]

\[\sin\left( \frac{7x}{2} \right) = 0\]

\[\frac{7x}{2} = \pi k\]

\[x = \frac{2}{7}\text{πk.}\]

\[\cos\left( \frac{9x}{2} \right) = 0\]

\[\frac{9x}{2} = \frac{\pi}{2} + \pi k\]

\[x = \frac{\pi}{9} + \frac{2}{9}\text{πk.}\]

\[Ответ:\ \frac{\pi}{9} + \frac{2}{9}\pi k;\ \frac{2}{7}\text{πk.}\]

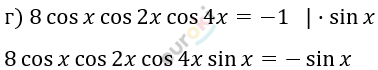
\[4\sin{2x}\cos{2x}\cos{4x} = - \sin x\]

\[2\sin{4x}\cos{4x} = - \sin x\]

\[\sin{8x} + \sin x = 0\]

\[2\sin\left( \frac{9}{2}x \right)\cos\left( \frac{7}{2}x \right) = 0\]

\[\sin\left( \frac{9x}{2} \right) = 0\]

\[\frac{9x}{2} = \pi n\]

\[x = \frac{2}{9}\text{πn.}\]

\[\cos\left( \frac{7x}{2} \right) = 0\]

\[\frac{7x}{2} = \frac{\pi}{2} + \pi m\]

\[x = \frac{\pi}{7} + \frac{2}{7}\text{πm.}\]

\[Ответ:\ x = \frac{2}{9}\pi n;\ \ \frac{\pi}{7} + \frac{2}{7}\text{πm.}\]