Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 11 класс Никольский Параграф 10. Равносильность уравнений на множествах Задание 16
Задание 16
\[\boxed{\mathbf{16}\mathbf{.}}\]
\[x - 1 \neq 0\]
\[x \neq 1.\]
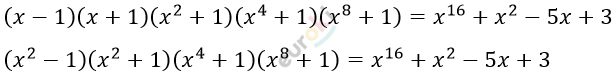
\[\left( x^{4} - 1 \right)\left( x^{4} + 1 \right)\left( x^{8} + 1 \right) =\]
\[= x^{16} + x^{2} - 5x + 3\]
\[\left( x^{8} - 1 \right)\left( x^{8} + 1 \right) =\]
\[= x^{16} + x^{2} - 5x + 3\]
\[x^{16} - 1 = x^{16} + x^{2} - 5x + 3\]
\[x^{2} - 5x + 4 = 0\]
\[x_{1} + x_{2} = 5;\ \ x_{1} \cdot x_{2} = 4\]
\[x_{1} = 1\ (не\ подходит);\]
\[x_{2} = 4.\]
\[Ответ:x = 4.\]
\[x + 1 \neq 0\]
\[x \neq - 1.\]
\[\left( x^{4} - 1 \right)\left( x^{4} + 1 \right)\left( x^{8} + 1 \right) =\]
\[= x^{16} + x^{2} + 5x + 3\]
\[\left( x^{8} - 1 \right)\left( x^{8} + 1 \right) =\]
\[= x^{16} + x^{2} + 5x + 3\]
\[x^{16} - 1 = x^{16} + x^{2} + 5x + 3\]
\[x^{2} + 5x + 4 = 0\]
\[x_{1} + x_{2} = - 5;\ \ x_{1} \cdot x_{2} = 4\]
\[x_{1} = - 1\ (не\ подходит);\]
\[x_{2} = - 4.\]
\[Ответ:x = - 4.\]
