Решебник по алгебре 11 класс Никольский Параграф 9. Равносильность уравнений и неравенств системам Задание 64

\(\boxed{\mathbf{64.}}\)

\[\textbf{а)}\log_{x}\frac{14x - 9}{8x + 13} \leq \log_{x}\frac{8x - 17}{8x + 13}\]

\[1)\ \left\{ \begin{matrix} 0 < \frac{14x - 9}{8x + 13} \leq \frac{8x - 17}{8x + 13} \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{14x - 9}{8x + 13} - \frac{8x - 17}{8x + 13} \leq 0 \\ \frac{14x - 9}{8x + 13} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{6x - 2}{8x + 13} \leq 0 \\ \frac{14x - 9}{8x + 13} > 0 \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\left\{ \begin{matrix} 6x - 2 \leq 0\ \ \ \\ 8x + 13 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{3}\text{\ \ \ \ \ \ \ } \\ x > - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[- \frac{13}{8} < x \leq \frac{1}{3}.\]

\[\left\{ \begin{matrix} 6x - 2 \geq 0\ \ \ \\ 8x + 13 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{3}\text{\ \ \ \ } \\ x < - \frac{1}{3} \\ \end{matrix} \right.\ \]

\[нет\ решений.\]

\[x \in \left( - \frac{13}{8};\frac{1}{3} \right\rbrack.\]

\[2.\ \left\{ \begin{matrix} 14x - 9 > 0 \\ 8x + 13 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{9}{14}\text{\ \ \ \ \ } \\ x > - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[x > \frac{9}{14}.\]

\[\left\{ \begin{matrix} 14x - 9 < 0 \\ 8x + 13 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{9}{14}\text{\ \ \ \ } \\ x < - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[x \in \left( - \infty; - \frac{13}{8} \right) \cup \left( \frac{9}{14}; + \infty \right).\]

\[Решение\ первой\ системы\ \]

\[в\ совокупности:\]

\[нет\ решений.\]

\[2)\ \left\{ \begin{matrix} \frac{14x - 9}{8x + 13} \geq \frac{8x - 17}{8x + 13} > 0 \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{14x - 9 - 8x + 7}{8x + 13} \geq 0 \\ \frac{8x - 17}{8x + 13} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{6x - 2}{8x + 13} \geq 0 \\ \frac{8x - 17}{8x + 13} > 0 \\ 0 < x < 1\ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 6x - 2 \geq 0\ \ \ \\ 8x + 13 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{3}\text{\ \ \ \ \ \ \ } \\ x > - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[x \geq \frac{1}{3}.\]

\[\left\{ \begin{matrix} 6x - 2 \leq 0\ \ \\ 8x + 13 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{3}\text{\ \ \ \ \ \ \ } \\ x < - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[x < - \frac{13}{8}.\]

\[x \in \left( - \infty - \frac{13}{8} \right) \cup \left\lbrack \frac{1}{3}; + \infty \right).\]

\[2.\ \left\{ \begin{matrix} 8x - 7 > 0\ \ \\ 8x + 13 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{7}{8}\text{\ \ \ \ \ \ \ } \\ x > - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[x > \frac{7}{8}.\]

\[\left\{ \begin{matrix} 8x - 7 < 0\ \ \\ 8x + 13 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{7}{8}\text{\ \ \ \ \ \ } \\ x < - \frac{13}{8} \\ \end{matrix} \right.\ \]

\[x < - \frac{13}{8}.\]

\[Решение\ второй\ системы\ \]

\[в\ совокупности:\]

\[x \in \left( \frac{7}{8};1 \right).\]

\[Объединим\ полученные\ \]

\[результаты:\]

\[x \in \left( \frac{7}{8};1 \right).\]

\[Ответ:\ x \in \left( \frac{7}{8};1 \right).\]

\[\textbf{б)}\log_{x}\frac{17x - 10}{9x + 14} \leq \log_{x}\frac{9x - 8}{9x + 14}\]

\[1)\ \left\{ \begin{matrix} 0 < \frac{17x - 10}{9x + 14} \leq \frac{9x - 8}{9x + 14} \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{17x - 10 - 9x + 8}{9x + 14} \leq 0 \\ \frac{17x - 10}{9x + 14} < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{8x - 2}{9x + 14} \leq 0\ \ \\ \frac{17x - 10}{9x + 14} < 0 \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 8x - 2 \leq 0\ \ \ \\ 9x + 14 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{4}\text{\ \ \ \ \ \ } \\ x > - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[- \frac{14}{9} < x \leq \frac{1}{4}.\]

\[\left\{ \begin{matrix} 8x - 2 \geq 0\ \\ 9x + 14 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{4}\text{\ \ \ \ \ \ } \\ x < - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[нет\ решений.\]

\[x \in \left( - \frac{14}{9};\frac{1}{4} \right\rbrack.\]

\[2.\ \left\{ \begin{matrix} 17x - 10 > 0 \\ 9x + 14 > 0\ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{10}{17}\text{\ \ \ } \\ x > - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[x > \frac{10}{17}.\]

\[\left\{ \begin{matrix} 17x - 10 < 0 \\ 9x + 14 < 0\ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{10}{17}\text{\ \ \ \ } \\ x < - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[x < - \frac{14}{9}.\]

\[x \in \left( - \infty; - \frac{14}{9} \right) \cup \left( \frac{10}{17}; + \infty \right).\]

\[Решение\ первой\ системы\ \]

\[в\ совокупности:\]

\[нет\ решений.\]

\[2)\ \left\{ \begin{matrix} \frac{17x - 10}{9x + 14} \geq \frac{9x - 8}{9x + 14} > 0 \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{17x - 10 - 9x + 8}{9x + 14} \geq 0 \\ \frac{9x - 8}{9x + 14} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{8x - 2}{9x + 14} \geq 0 \\ \frac{9x - 8}{9x + 14} > 0 \\ 0 < x < 1\ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 8x - 2 \geq 0\ \ \\ 9x + 14 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{4}\text{\ \ \ \ \ \ \ } \\ x > - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[x \geq \frac{1}{4}.\]

\[\left\{ \begin{matrix} 8x - 2 \leq 0\ \ \ \\ 9x + 14 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{4}\text{\ \ \ \ \ \ \ } \\ x < - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[x < - \frac{14}{9}.\]

\[x \in \left( - \infty; - \frac{14}{9} \right) \cup \left\lbrack \frac{1}{4}; + \infty \right).\]

\[2.\ \left\{ \begin{matrix} 9x - 8 > 0\ \ \\ 9x + 14 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{8}{9}\text{\ \ \ \ \ \ } \\ x > - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[x > \frac{8}{9}.\]

\[\left\{ \begin{matrix} 9x - 8 < 0\ \ \\ 9x + 14 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{8}{9}\text{\ \ \ \ \ \ \ } \\ x < - \frac{14}{9} \\ \end{matrix} \right.\ \]

\[x < - \frac{14}{9}.\]

\[x \in \left( - \infty; - \frac{14}{9} \right)\left( \frac{8}{9}; + \infty \right).\]

\[Решение\ второй\ системы:\]

\[x \in \left( \frac{8}{9};1 \right).\]

\[Объединим\ полученные\ \]

\[результаты:\]

\[x \in \left( \frac{8}{9};1 \right).\]

\[Ответ:\ x \in \left( \frac{8}{9};1 \right).\]

\[\textbf{в)}\log_{x}\frac{20x - 11}{6x + 11} \leq \log_{x}\frac{10x - 9}{6x + 11}\]

\[1)\ \left\{ \begin{matrix} 0 < \frac{20x - 11}{6x + 11} \leq \frac{10x - 9}{6x + 11} \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{20x - 11 - 10x + 9}{6x + 11} \leq 0 \\ \frac{20x - 11}{6x + 11} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{10x - 2}{6x + 11} \leq 0\ \ \\ \frac{20x - 11}{6x + 11} > 0 \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 10x - 2 \leq 0 \\ 6x + 11 > 0 \\ \end{matrix} \right.\ \ \]

\[\ \left\{ \begin{matrix} x \leq \frac{1}{5}\text{\ \ \ \ \ \ } \\ x > - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[- \frac{11}{6} < x \leq \frac{1}{5}.\]

\[\ \left\{ \begin{matrix} 10x - 2 \geq 0 \\ 6x + 11 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{5}\text{\ \ \ \ \ \ } \\ x < - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[нет\ решений.\]

\[x \in \left( - \frac{11}{6};\frac{1}{5} \right\rbrack.\]

\[2.\ \ \left\{ \begin{matrix} 20x - 11 > 0 \\ 6x + 11 > 0\ \ \\ \end{matrix} \right.\ \]

\[\ \left\{ \begin{matrix} x > \frac{11}{20}\text{\ \ \ } \\ x > - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[x > \frac{11}{20}.\]

\[\left\{ \begin{matrix} 20x - 11 < 0 \\ 6x + 11 < 0\ \ \\ \end{matrix} \right.\ \]

\[\ \left\{ \begin{matrix} x < \frac{11}{20}\text{\ \ } \\ x < - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[x < - \frac{11}{6}.\]

\[Решение\ первой\ системы\ \]

\[совокупности:\]

\[нет\ решений.\]

\[2)\ \left\{ \begin{matrix} \frac{20x - 11}{6x + 11} \geq \frac{10x - 9}{6x + 11} > 0 \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{20x - 11 - 10x + 9}{6x + 11} \geq 0 \\ \frac{10x - 9}{6x + 11} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{10x - 2}{6x + 11} \geq 0 \\ \frac{10x - 9}{6x + 11} > 0 \\ 0 < x < 1\ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 10x - 2 \geq 0 \\ 6x + 11 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{5}\text{\ \ \ \ \ } \\ x > - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[x \geq \frac{1}{5}.\]

\[\left\{ \begin{matrix} 10x - 2 \leq 0 \\ 6x + 11 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{5}\text{\ \ \ \ \ \ } \\ x < - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[x < - \frac{11}{6}.\]

\[x \in \left( - \infty - \frac{11}{6} \right) \cup \left\lbrack \frac{1}{5}; + \infty \right).\]

\[2.\ \left\{ \begin{matrix} 10x - 9 > 0 \\ 6x + 11 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{9}{10}\text{\ \ \ } \\ x > - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[x > \frac{9}{10}.\]

\[\left\{ \begin{matrix} 10x - 9 < 0 \\ 6x + 11 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{9}{10}\text{\ \ \ \ } \\ x < - \frac{11}{6} \\ \end{matrix} \right.\ \]

\[x < - \frac{11}{6}.\]

\[x \in \left( - \infty; - \frac{11}{6} \right) \cup \left( \frac{9}{10}; + \infty \right).\]

\[Решение\ второй\ системы\ \]

\[совокупности:\]

\[x \in \left( \frac{9}{10};1 \right).\]

\[Объединим\ полученные\ \]

\[результаты:\]

\[x \in \left( \frac{9}{10};1 \right).\]

\[Ответ:\ x \in \left( \frac{9}{10};1 \right).\]

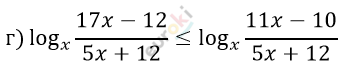
\[1)\ \left\{ \begin{matrix} 0 < \frac{17x - 12}{5x + 12} \leq \frac{11x - 10}{5x + 12} \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{17x - 12 - 11x + 10}{5x + 12} \leq 0 \\ \frac{17x - 12}{5x + 12} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{6x - 2}{5x + 12} \leq 0\ \ \\ \frac{17x - 12}{5x + 12} > 0 \\ x > 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 6x - 2 \leq 0\ \ \\ 5x + 12 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{3}\text{\ \ \ \ \ \ } \\ x > - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[- \frac{12}{5} < x \leq \frac{1}{3}.\]

\[\left\{ \begin{matrix} 6x - 2 \geq 0\ \ \\ 5x + 12 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{3}\text{\ \ \ \ \ \ \ } \\ x < - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[нет\ решений.\]

\[x \in \left( - \frac{12}{5};\frac{1}{3} \right\rbrack.\]

\[2.\ \left\{ \begin{matrix} 17x - 12 > 0 \\ 5x + 12 > 0\ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{12}{17}\text{\ \ \ \ } \\ x > - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[x > \frac{12}{17}.\]

\[\left\{ \begin{matrix} 17x - 12 < 0 \\ 5x + 12 < 0\ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{12}{17}\text{\ \ \ } \\ x < - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[x < - \frac{12}{5}.\]

\[x \in \left( - \infty; - \frac{12}{5} \right) \cup \left( \frac{12}{17}; + \infty \right).\]

\[Решение\ первой\ системы\ \]

\[совокупности:\]

\[не\ имеет\ решений.\]

\[2)\ \left\{ \begin{matrix} \frac{17x - 12}{5x + 12} \geq \frac{11x - 10}{5x + 12} > 0 \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{17x - 12 - 11x + 10}{5x + 12} \geq 0 \\ \frac{11x - 10}{5x + 12} > 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 0 < x < 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{6x - 2}{5x + 12} \geq 0\ \ \ \\ \frac{11x - 10}{5x + 12} > 0 \\ 0 < x < 1\ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[1.\ \left\{ \begin{matrix} 6x - 2 \geq 0\ \ \ \\ 5x + 12 > 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \geq \frac{1}{3}\text{\ \ \ \ \ \ } \\ x > - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[x \geq \frac{1}{3}.\]

\[\left\{ \begin{matrix} 6x - 2 \leq 0\ \ \ \\ 5x + 12 < 0 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x \leq \frac{1}{3}\text{\ \ \ \ \ \ } \\ x < - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[x < - \frac{12}{5}.\]

\[x \in \left( - \infty; - \frac{12}{5} \right) \cup \left\lbrack \frac{1}{3}; + \infty \right).\]

\[2.\ \left\{ \begin{matrix} 11x - 10 > 0 \\ 5x + 12 > 0\ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{10}{11}\text{\ \ \ \ } \\ x > - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[x > \frac{10}{11}.\]

\[\left\{ \begin{matrix} 11x - 10 < 0 \\ 5x + 12 < 0\ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x < \frac{10}{11}\text{\ \ \ \ } \\ x < - \frac{12}{5} \\ \end{matrix} \right.\ \]

\[x \in \left( - \infty; - \frac{12}{5} \right) \cup \left( \frac{10}{11}; + \infty \right).\]

\[Решение\ второй\ системы\ \]

\[совокупности:\]

\[x \in \left( \frac{10}{11};1 \right).\]

\[Объединим\ полученные\ \]

\[результаты:\]

\[x \in \left( \frac{10}{11};1 \right).\]

\[Ответ:\ x \in \left( \frac{10}{11};1 \right).\]